413. Коллинеарны ли векторы: а) а{3; 6; 8} и b{6; 12; 16); б) с{1; — 1; 3} и d {2; 3; 15}; в) i{1; 0; 0} и j{0; 1; 0}; г) m {0; 0; 0} и n {5; 7; -3}; д) p {⅓ -1; 5} и q {-1; -3; -15}?

Решение, а) Координаты вектора а {3; 6; 8} пропорциональны координатам вектора b{6; 12; 16}: где k=½ Поэтому a=kb, и, следовательно, векторы а и b коллинеарны. б) Координаты вектора с{ 1; —1; 3} не пропорциональны координатам вектора d {2; 3; 15}, например ½≠-⅓ Поэтому векторы с и d не коллинеарны. В самом деле, если предположить, что векторы с и d коллинеарны, то существует такое число k, что c = kd. Но тогда координаты вектора с пропорциональны координатам вектора d, что противоречит условию задачи. а) Координаты вектора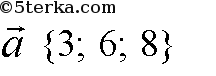

и вектора

пропорциональны:

где

Поэтому

, и, следовательно, векторы a и b коллинеарны.

б) Координаты вектора

и вектора

не

пропорциональны, например

Следовательно векторы c и d не коллинеарны.

в) Координаты вектора

и вектора

не

пропорциональны, следовательно, векторы i и j не коллинеарны.

г) Координаты вектора

и вектора

пропорциональны при k=0, следовательно, векторы m и n коллинеарны. m =0 коллинеарен любому вектору.

д) Координаты вектора

и вектора

не

пропорциональны, например

Поэтому векторы p и q не коллинеарны.