311. Основанием пирамиды DABC является треугольник со сторонами АС= 13 см, АВ = 15 см, СВ= 14 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 9 см. а) Найдите площадь полной поверхности пирамиды. б) Докажите, что основание перпендикуляр

311. Основанием пирамиды DABC является треугольник со сторонами АС= 13 см, АВ = 15 см, СВ= 14 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 9 см. а) Найдите площадь полной поверхности пирамиды. б) Докажите, что основание перпендикуляра, проведенного из вершины А к плоскости грани ВDC, лежит на высоте этой грани, и найдите длину этого перпендикуляра.

а) ΔDAC и ΔDAB— прямоугольные.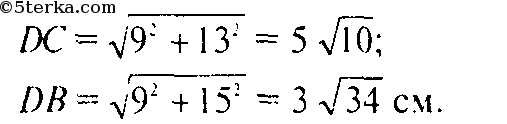

Проведем высоту АН в ΔАВС. Тогда DH — высота ΔBDC по теореме о трех перпендикулярах.

Найдем АН: Пусть ВН = х.

б) Предположим, что основание перпендикуляра AA₁ не попадает на прямую DH. Тогда ВС ⊥ DA₁A и BC⊥ADH, т.к. ВС⊥DА и BC⊥AA₁ в первом случае и ВС⊥DH во втором. Но тогда через AD проходят две плоскости, перпендикулярные к ВС. Это невозможно, поэтому А₁ лежит на DH.

Рассмотрим ΔDAH: DА = 9см, АН= 12см, DH= 15 см