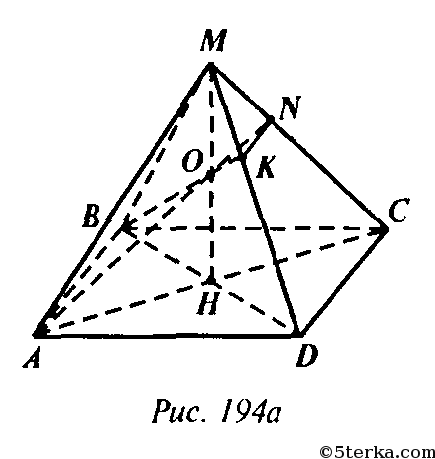
Докажем, что

Действительно:
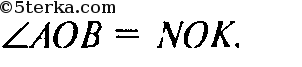
Докажем, что

Рассмотрим
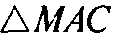
(рис. 194б). Проведем OO' — среднюю линию ΔMHC и ОЕ — параллельно АС. Тогда из того, что
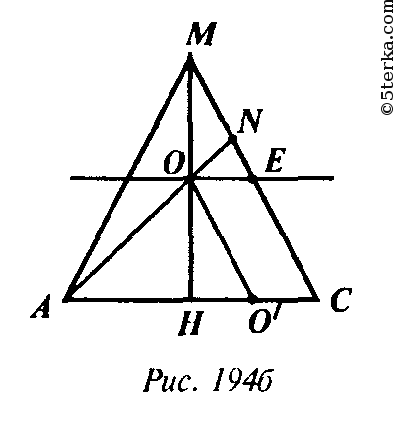
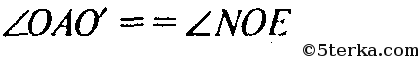
и

следует, что

Значит

но

(так как ОЕСО' — параллелограмм), а


Поэтому

Аналогично рассматривая ΔMBD получаем, что
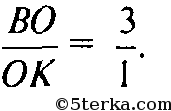
Поэтому
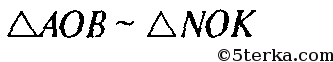
и коэффициент подобия равен 3. Так как АВ = 6 дм, то NK = 2 дм. Очевидно, что АВ || NK. Поэтому ABNK — трапеция. Проведем высоту FOG трапеции ABNK через точку О (рис. 195).

Тогда из подобия треугольников AOB и NOK следует, что

Таким образом:

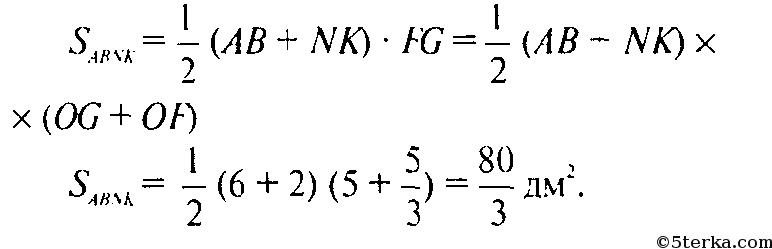
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №309
к главе «Глава III Многогранники. Дополнительные задачи ».
Комментарии