260. В правильной треугольной пирамиде DABC через боковое ребро DC и высоту DO пирамиды проведена плоскость α. Докажите, что: а) ребро АВ перпендикулярно к плоскости α; б) перпендикуляр, проведенный из вершины С к апофеме грани ADB, является п

260. В правильной треугольной пирамиде DABC через боковое ребро DC и высоту DO пирамиды проведена плоскость α. Докажите, что: а) ребро АВ перпендикулярно к плоскости α; б) перпендикуляр, проведенный из вершины С к апофеме грани ADB, является перпендикуляром к плоскости ADB.

Проведем прямую СО. СО пересечет AB в точке Н. Так как О — центр треугольника ABC, то СН ⊥ АВ и АН = ВН. Но тогда DH — медиана, а следовательно, и высота равнобедренного треугольника ADB, т. е. DH апофема грани ADB.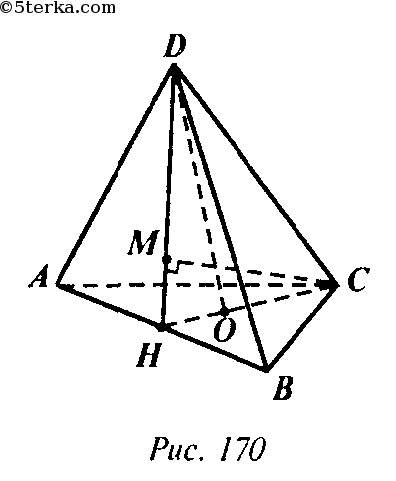

а) АВ ⊥ СН, АВ ⊥ DH значит прямая АВ перпендикулярна плоскости α по признаку перпендикулярности прямой и плоскости. б)Перпендикуляр CM к апофеме грани ADB лежит в плоскости CDH, поэтому СМ ⊥ АВ. Но СМ ⊥ DН, поэтому по признаку перпендикулярности прямой и плоскости CM ⊥ ADB.