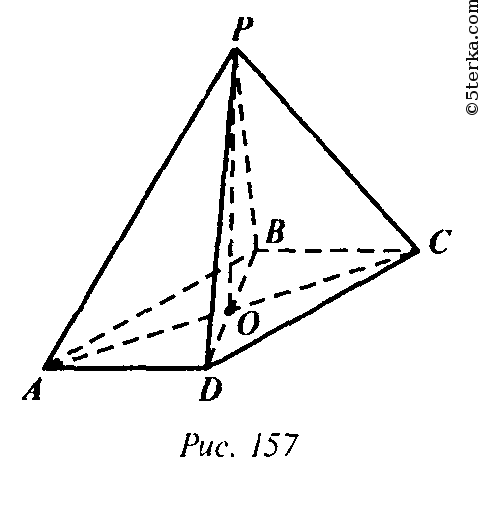
Аналогично PB⊥ВС. Найдем PD:
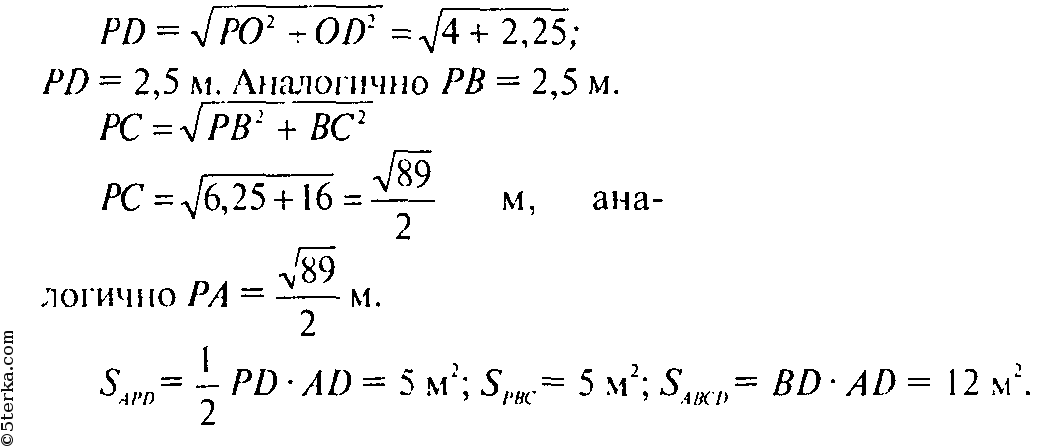
Найдем SPAB и SPDC: так как ΔPAB=ΔPDC ( по трем сторонам), то достаточно найти площадь одного из треугольников. Рассмотрим ΔPDC: проведем высоту PH (рис. 158).
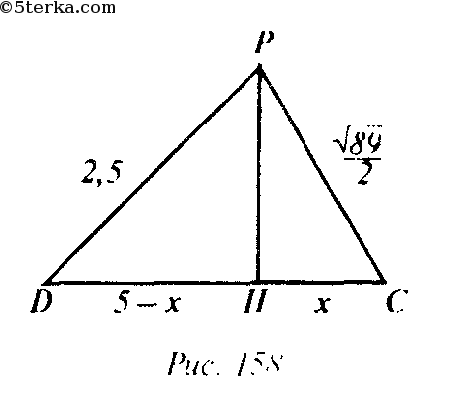
Пусть
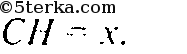
Тогда
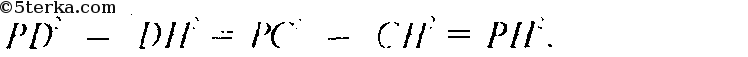
Таким образом
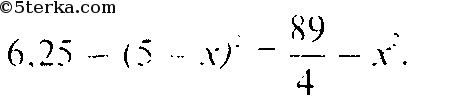
Отсюда
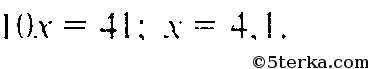
Тогда
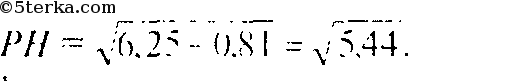
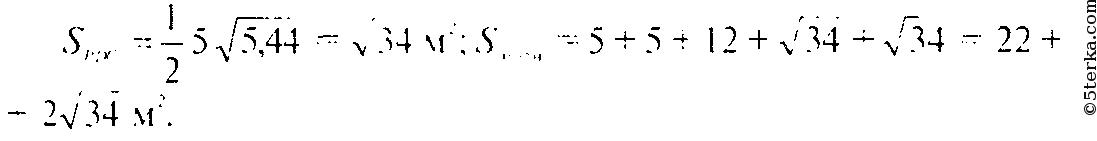
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №241
к главе «Глава III Многогранники. § 2. Пирамида».
Комментарии