* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Решение:
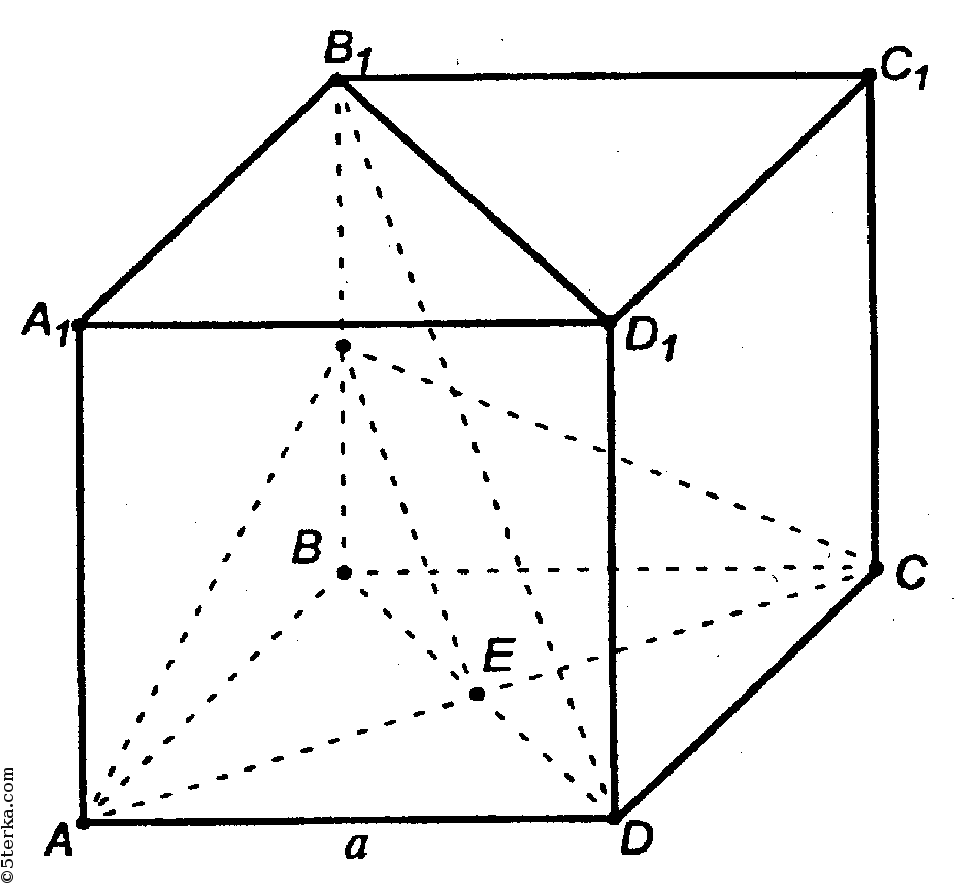
а) Найдем, например, р(АА1, B1D).

поэтому

Проводим

Важно заметить, что в силу свойств куба точка Е будет серединой BD, то есть центром нижней грани куба.

б) Проводим через АС плоскость, параллельную B1D. Для этого проведем в плоскости BB1D прямую EK || B1D. Соединим А и K, С и K; пл. AKC || B1D по теореме I.
Рассмотрим BB1D.


KE - средняя линия в ΔBB1D. Искомое расстояние х = ЕМ, ЕМ ⊥ B1D по построению.
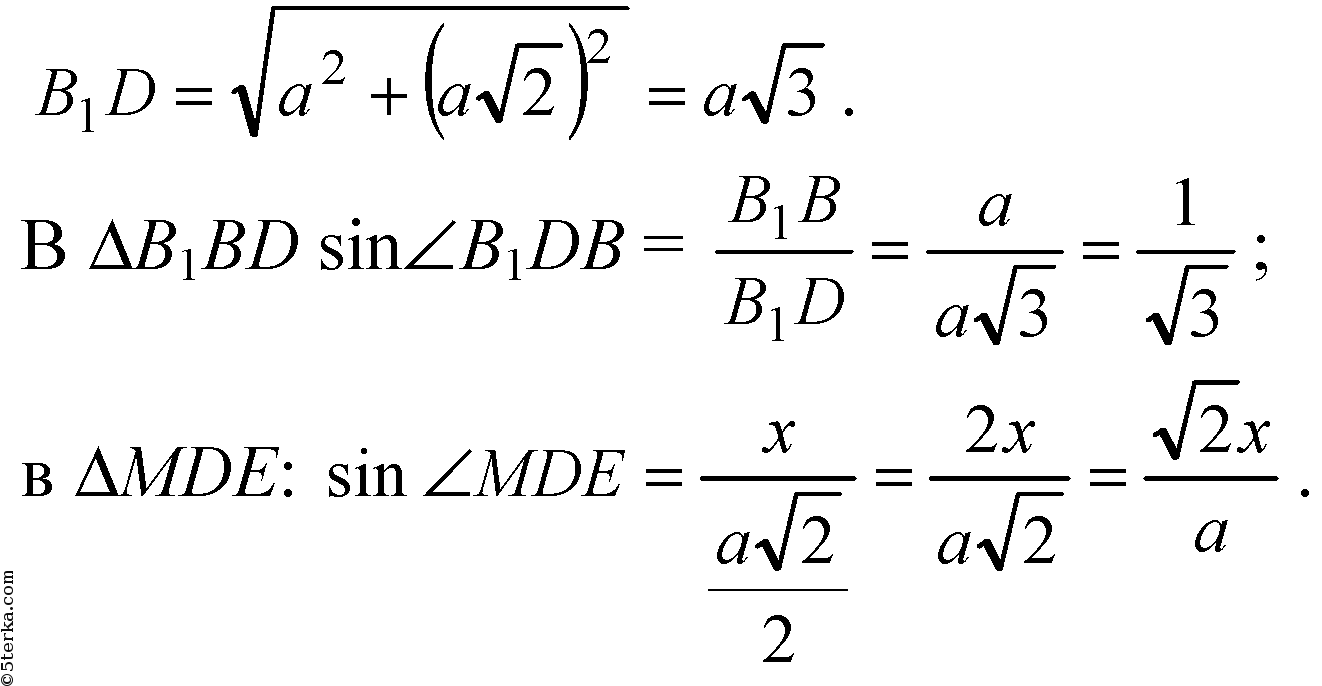
Получим уравнение:

Ответ:

 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №194
к главе «Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей.».