157. Прямая ОК перпендикулярна к плоскости ромба ABCD, диагонали которого пересекаются в точке О. а) Докажите, что расстояния от точки К до всех прямых, содержащих стороны ромба, равны, б) Найдите это расстояние, если ОК = 4,5 дм, АС = 6 дм, BD = 8 дм.

Дано:

Решение:
В (ABCD) проведем через т. О EF ⊥ AD, ОН ⊥ CD.

Диагонали ромба, во-первых, являются биссектрисами его углов; во-вторых, в точке пересечения делятся пополам. Следовательно,


отсюда


утверждение а)
доказано. Оно следует из равенства треугольников. (KO общий катет,
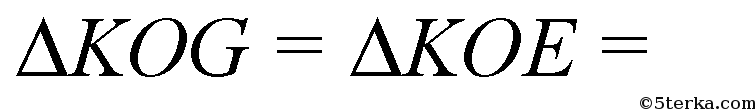

отсюда
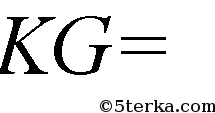


С другой стороны,

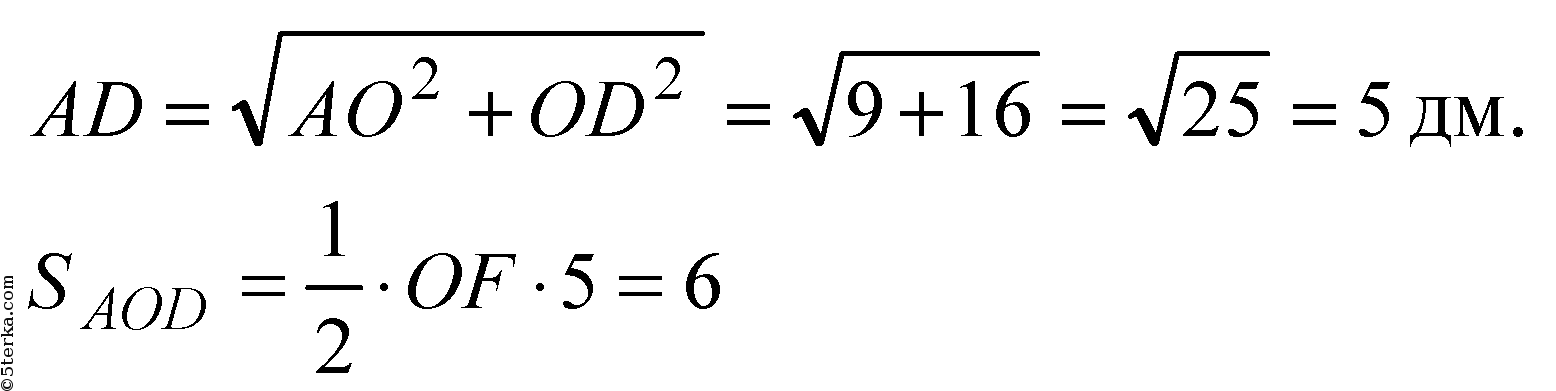
Отсюда

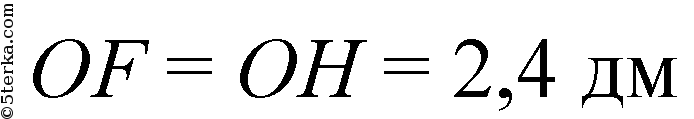
(из равенства ΔOFD и ΔOHD).
Из ΔKOH:

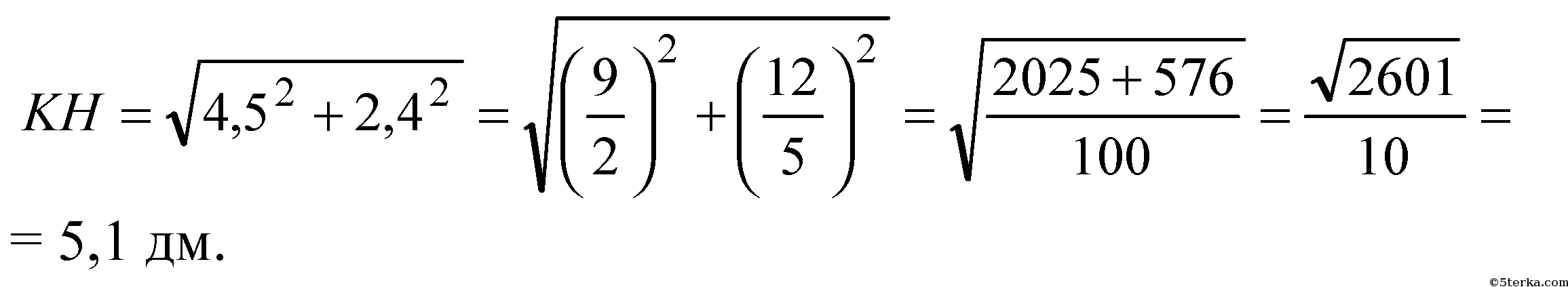
Ответ: б)
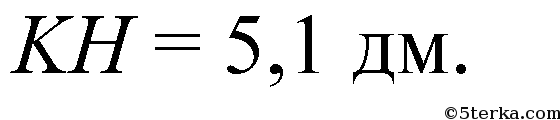
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №157
к главе «Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью.».
Комментарии