150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что KD = 6 см, КВ = 7 см, КС=9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника ABCD; б) расстояние между прямыми АК и CD.
Дано:
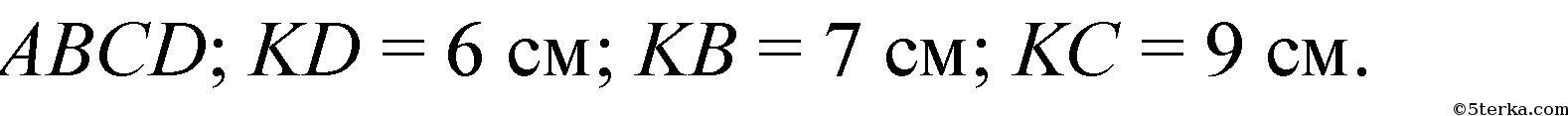
Решение
а)
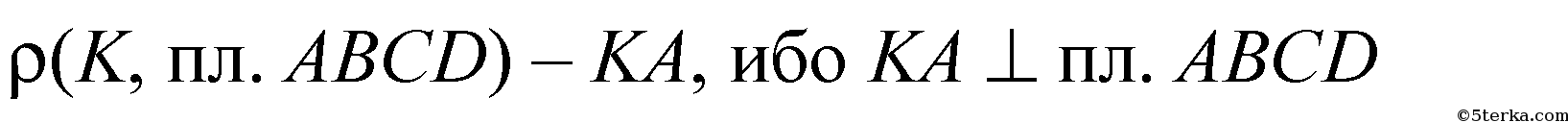
- по условию.
ΔKDC - прямоугольный,
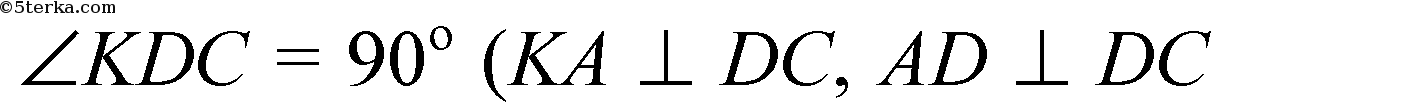
- по
теореме о 3-х перпендикулярах KD ⊥ DC).
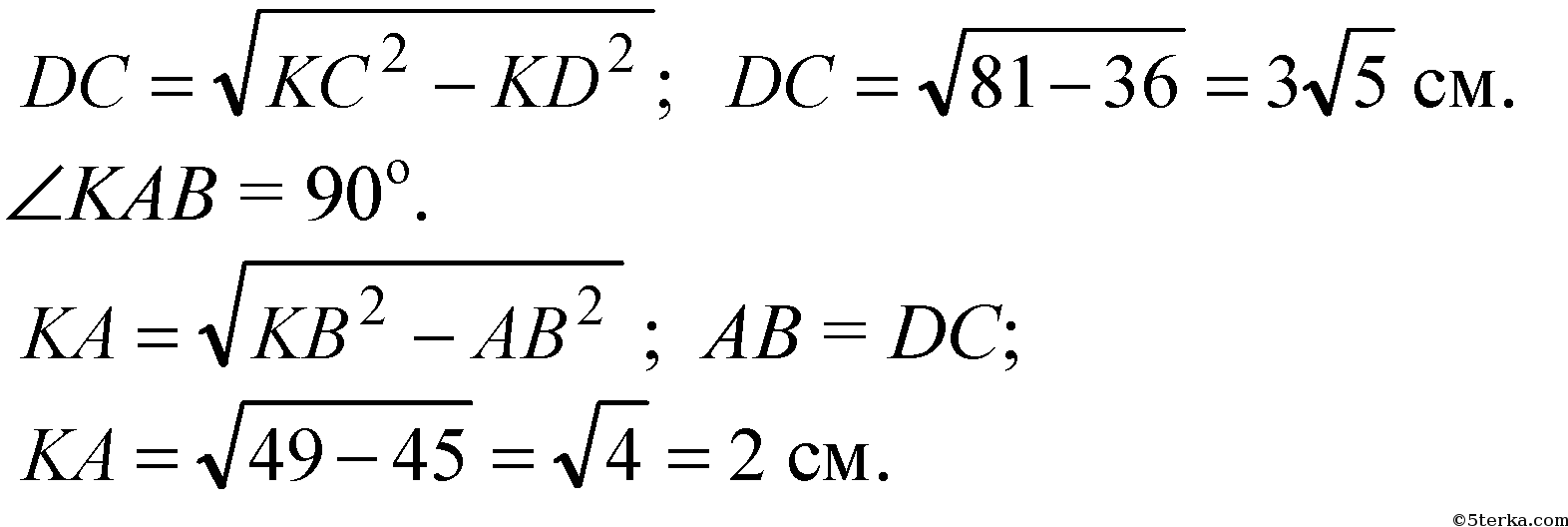
б) Плоскость KAB || DC, т.к. DC || AB. Расстояние между двумя скрещивающимися прямыми p(AK, CD) = DA, ведь DA ⊥ пл. KAB.
Из ΔDAK
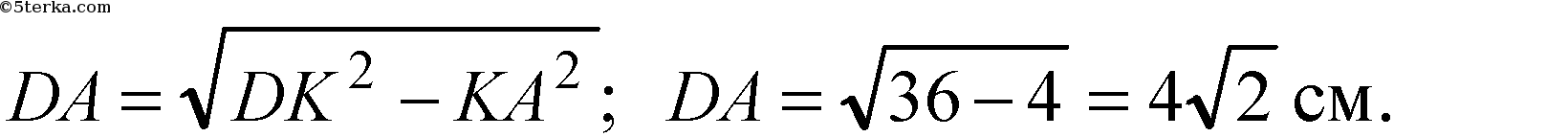
Ответ:
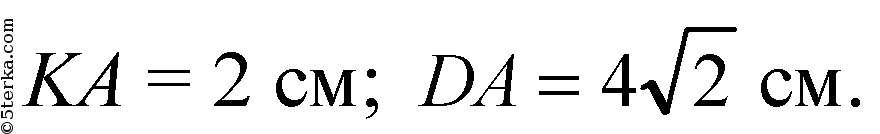
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №150
к главе «Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью.».
Комментарии