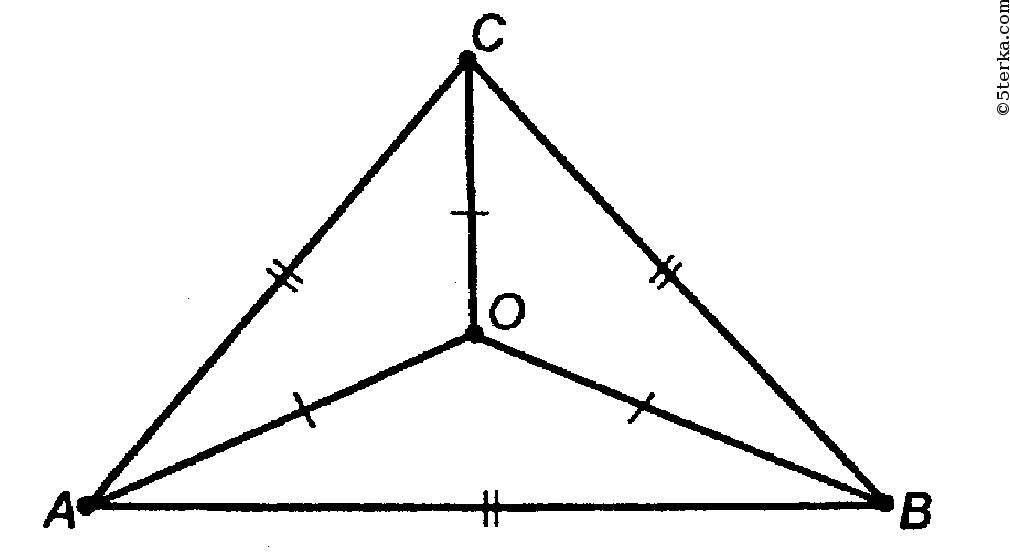
122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этого треугольника проведена прямая ОК, параллельная прямой CD. Известно, что АВ = 16 √3 см, ОK = 12 см, CD = 16 см. Найдите расстояния от точек D и К до вершин А и В треугольника.
Решение:
Рассмотрим ΔDAC и ΔDCB.
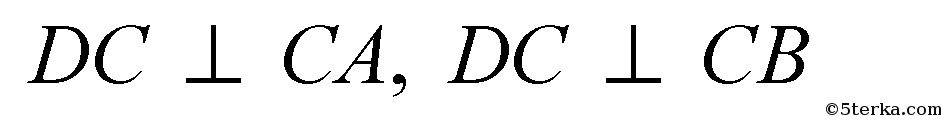
- по условию,
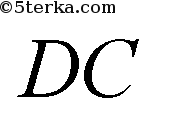
- общая,
то
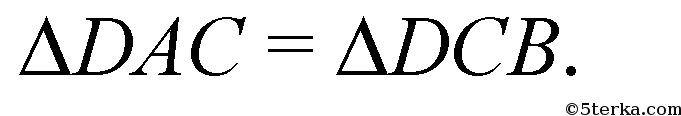
Отсюда
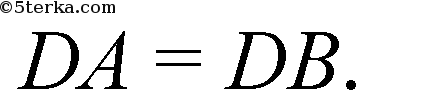
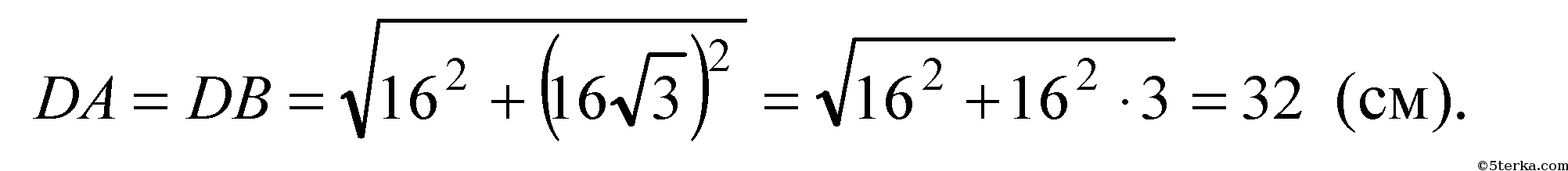
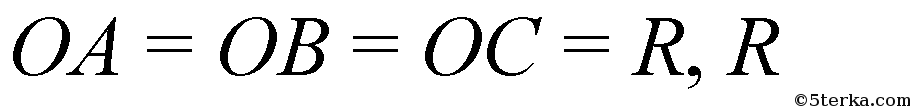
- радиус описанной окружности.
(следствие из теоремы синусов);
Итак,
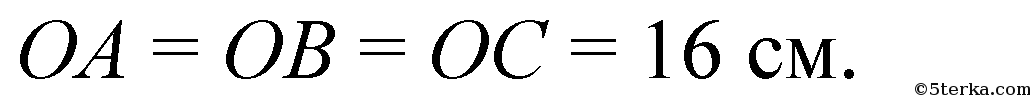
Итак,
ΔKOA = ΔKOB (прямоугольные, равны по двум катетам), следовательно, AK = KB.
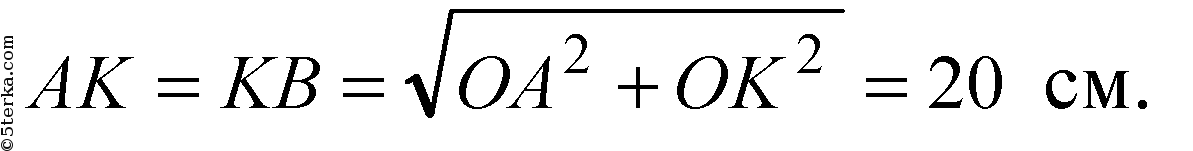
Ответ:
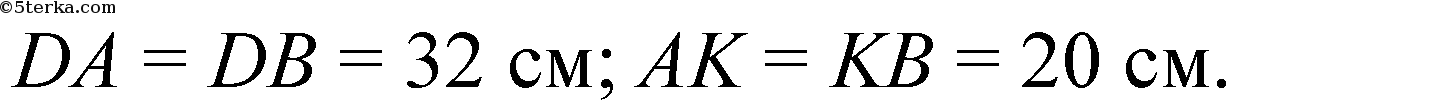
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №122
к главе «Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости».
Комментарии