74. Через точку пересечения медиан грани BCD тетраэдра ABCD проведена плоскость, параллельная грани ABC. а) Докажите, что сечение тетраэдра этой плоскостью есть треугольник, подобный треугольнику ABC. б) Найдите отношение площадей сечения и треугольника ABC.

Пусть т. О - точка пересечения медиан ΔBCD.
Плоскость сечения имеет с гранью ADC общую т. N, значит, обе плоскости пересекаются по прямой, проходящей через т. N.
Плоскость сечения и параллельная ей пл. АВС пересекаются плоскостью ADC, значит линии пересечения параллельны,

Аналогично,


(по первому признаку).
Утверждение а) доказано. б)

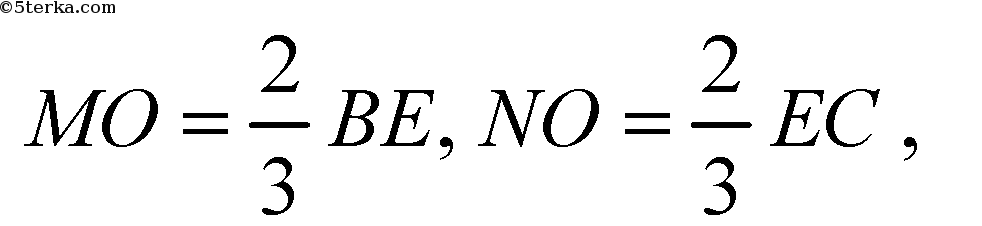
потому что:

и

Отношение площадей подобных фигур равно отношению квадратов соответствующих линейных размеров.

Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №74
к главе «Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед.».
Комментарии