33. Докажите, что если три плоскости, не проходящие через одну прямую, попарно пересекаются, то прямые, по которым они пересекаются, либо параллельны, либо имеют общую точку.

Пусть а не параллельна b, тогда а пересекается с b в некоторой точке K.

Тогда плоскость γ пересекается с плоскостью α не только по прямой с, но еще по второй прямой, проходящей через т. К.

То есть точка

Получили, что либо плоскости имеют общую точку K

либо наше допущение неверно, то есть

Если

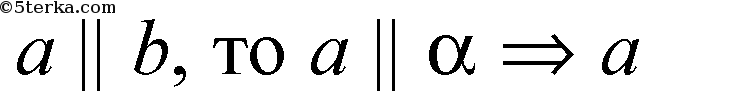
не пересекается с с, но лежит с ней в одной плоскости γ. Тогда по определению

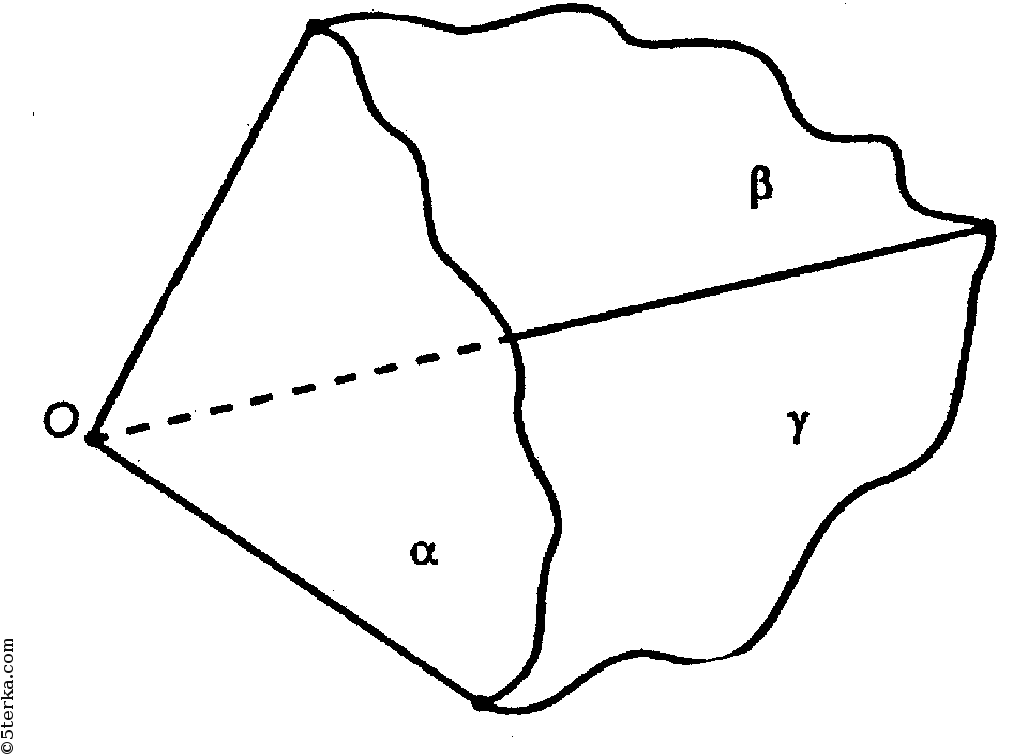
В случае, когда плоскости имеют общую точку, они попарно пересекаются, образуя фигуру, называемую трехгранным углом.