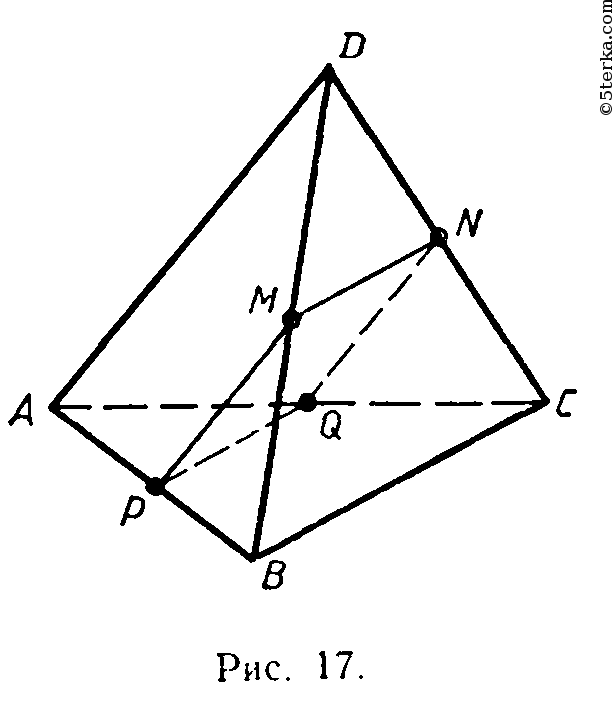
Поскольку
Из условий
по теореме п. 5 получим: PM || QN.
Отсюда следует, что P, Q, M и N лежат в 1 плоскости.
Получим, что MN и PQ - средние линии в ΔBDC и ΔABC, значит, MN || BC и PQ || BC. Имеем из теоремы п. 5 MN || PQ.
Значит, 4-угольник MNPQ - параллелограмм по определению (т.к. является плоским четырехугольником).
Ответ: 26 см.
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №17
к главе «Глава I Параллельность прямых и плоскостей. §1 Параллельность прямых, прямой и плоскости.».
Комментарии