№ 15. Докажите, что середины сторон правильного n-угольника являются вершинами другого правильного n-угольника. Пусть АВСDЕ — правильный n-угольник, АА1 = А1В, ВВ1 = В1С и т.д.

Рассмотрим ΔА₁ВВ₁ и ΔВ₁СС₁.

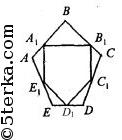
А₁В = В₁С, ВВ₁ = СС₁ (как половины равных сторон n-угольника); ∠В = ∠C (из условия). Значит, ΔА₁ВВ₁ = ΔВ₁СС₁, так

что А1В1 = В1С1.

Аналогично доказывается, что все стороны полученного n-угольника равны, то есть n-угольник — правильный.

Что и требовалось доказать.