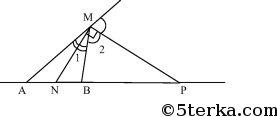
Возьмем произвольную точку М, такую что
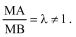
Проведем биссектрису MN и биссектрису внешнего угла
а следовательно геометрическое место точек, отношение расстояний от которых до двух данных точек постоянно и не равно 1 — это множество точек, из которых фиксированный отрезок (NP) виден под прямым углом, то есть окружность, построенная на диаметре NP. Что и требовалось доказать.
Источник:
Решебник
по
геометрии
за 9 класс (А.В.Погорелов, 2001 год),
задача №47
к главе «§11. Подобие фигур».
Комментарии