№ 30. Докажите, что у равнобедренного треугольника высота а, опущенная на основание, является медианой и биссектрисой.

Исходя из утверждения задачи № 29, выходит, что ΔABD = ΔDBC, таким образом, AD = DC как стороны, лежащие в равных треугольниках против равных углов, следовательно, BD — медиана.

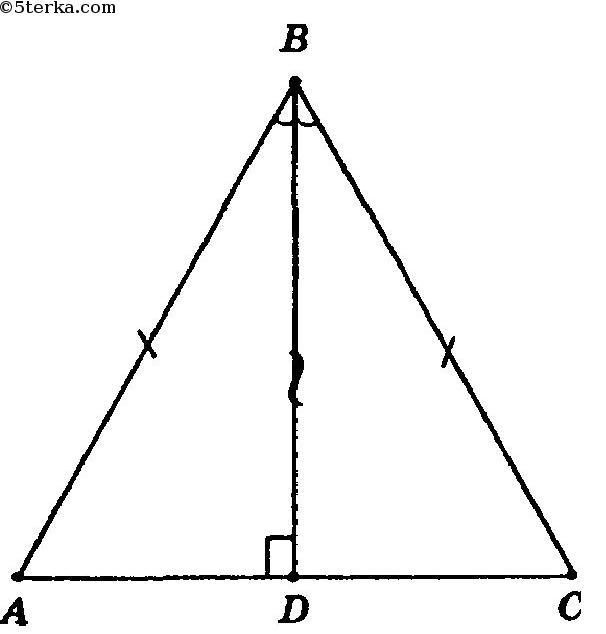
∠ABD = ∠DBC (следовательно, BD — биссектриса), что и требовалось доказать.