№ 18. 1) Докажите, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника. 2) Докажите, что середины сторон равностороннего треугольника являются также вершинами равностороннего треугольника.

1)

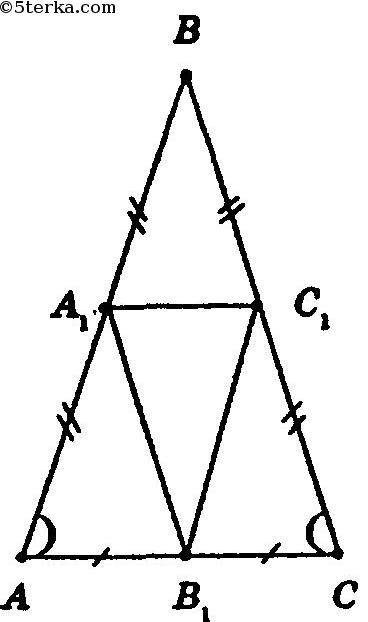
В ΔАА₁В₁ и ΔВ₁С₁С:

АА₁ = СС₁ как половины равных сторон (т.к. АА₁ = АВ : 2 = ВС : 2 = СС₁)

∠А = ∠С, т.к. ΔАВС — равнобедренный и ∠А и ∠С — углы при основании.

Таким образом, ΔАА₁В₁ = ΔВ₁С₁С по 1-му признаку равенства треугольников.

Отсюда А₁В₁ = В₁С₁.

Таким образом, ΔА₁В₁С₁ — равнобедренный (по определению).

2)

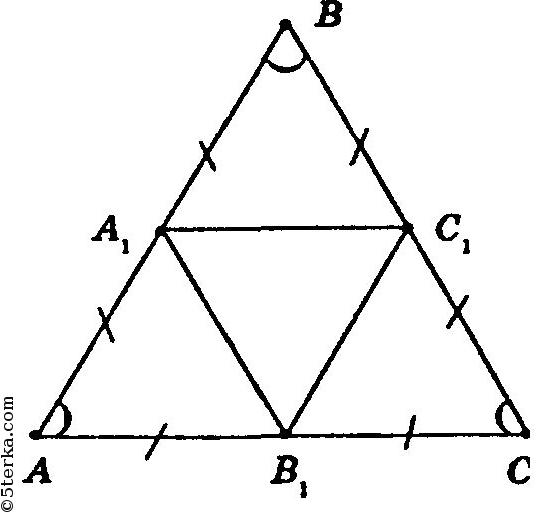
В ΔАА₁В₁, ΔА₁ВС₁, ΔСС₁В₁ ∠А = ∠В = ∠С (т.к. ΔАВС — равносторонний). АА₁ = А₁В = ВС₁ = С₁С = СВ₁ = В₁А (как половины равных сторон).

Таким образом, ΔАА₁В = ΔА₁ВС = ΔСС₁В₁ по 1-му признаку равенства треугольников. Откуда А₁С₁ = С₁В₁ = А₁В₁.

Таким образом, ΔА₁В₁С₁ равносторонний по определению.