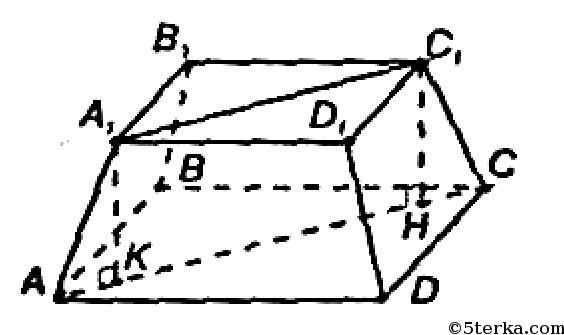
70. Высота правильной четырехугольной усеченной пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды.

Рассмотрим диагональное сечение АА₁С₁С, AA₁=CC₁ и A₁C₁||AC. Так что АА₁С₁С — равнобедренная трапеция.

A₁С₁ и АС — диагонали квадратов, лежащих в основании усеченной пирамиды. Значит,

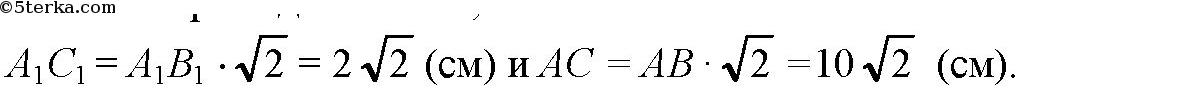
Так как

— прямоугольник и

Прямоугольные треугольники AA₁K и СС₁Н равны по гипотенузе и катету. Так что АК=СН. Тогда

Далее, по теореме Пифагора в ΔAA₁К:

Ответ: 9 см.

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №70
к главе «§ 20. Многогранники».

Все задачи

← 69. Докажите, что боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

71. Стороны оснований правильной усеченной треугольной пирамиды 4дм и 1дм. Боковое ребро 2 дм. Найдите высоту пирамиды. →

Комментарии