56. В правильной треугольной пирамиде с высотой h через сторону основания а проведена плоскость, пересекающая противолежащее боковое ребро под прямым углом. Найдите площадь сечения.

Пусть АВСS пирамида, АВС — правильный треугольник.

Плоскость ADC перпендикулярна ребру BS. Тогда треугольники ADB, CDB и MDB прямоугольные.

ΔADB = ΔCDB по гипотенузе и катету (АВ = ВС = а и DB — общий катет). Так что AD = DC.

Следовательно, ВМ и DM — медианы и высоты треугольников.

Тогда

(так как АВС — равносторонний).

Высота SH в правильной пирамиде проходит через центр окружности, описанной около основания.

Далее, в прямоугольном ΔSHB:

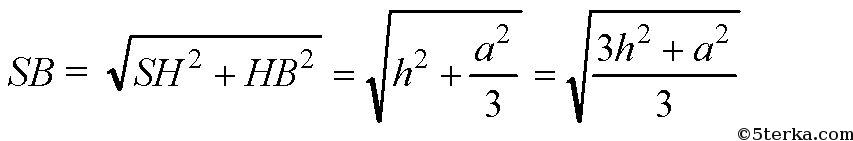
В прямоугольных ΔSHB и ΔMDB острый угол ∠SBM — общий. Значит, ΔSHB ~ ΔMDB по двум углам. Так что

откуда получаем, что

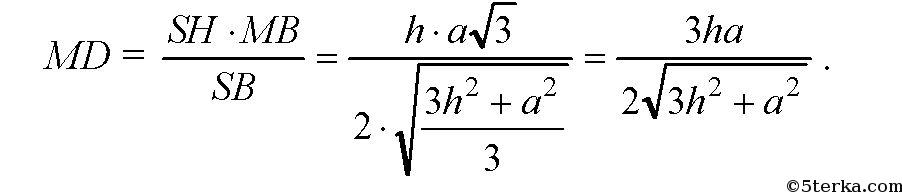
А площадь сечения находим по формуле: