Проведем SO — высоту пирамиды и перпендикуляры SK, SM и SN к соответствующим сторонам ΔАВС.
Тогда по теореме о трех перпендикулярах OK ⊥ ВС, ОМ ⊥ АС и ON ⊥ AB. Так что ∠SKO = ∠SMO = ∠SNO = 60° — линейные углы данных двугранных углов. Значит, треугольники SKO, SMO и SNO равны по катету и острому углу. Тогда OM = OK = ON, то есть точка О является центром окружности, вписанной в основание. В прямоугольном ΔAВС:
Тогда площадь ΔAВС равна:
С другой стороны, S = pr.
Так что
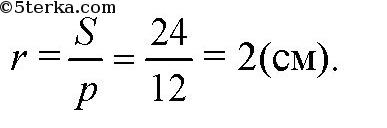
Далее, в ΔSMO:
Ответ:
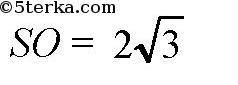
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №45
к главе «§ 20. Многогранники».
Комментарии