19. Сторона основания правильной четырехугольной призмы равна 15 см, высота равна 20 см. Найдите кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы.

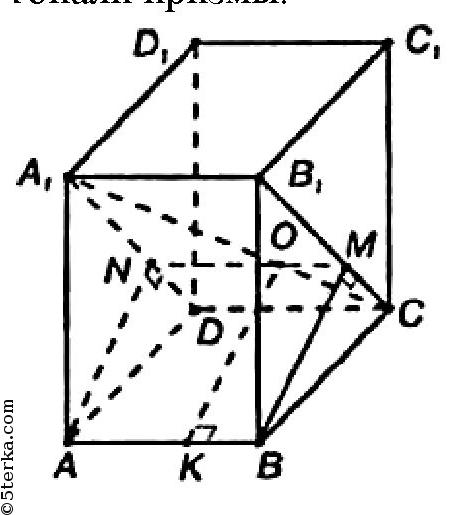
Проведем плоскость А₁В₁СD, а через ребро АВ проведем плоскость ABMN, перпендикулярную плоскости A₁B₁CD.

Так как АВ перпендикулярна боковым граням, то ABMN — прямоугольник.

Пусть О — точка пересечения АС и MN. Проведем ОК ⊥ АВ. Тогда ОК=ВМ.

В прямоугольном ΔВВ₁С:

(по теореме Пифагора). Тогда площадь ΔВВ₁С:

С другой стороны,

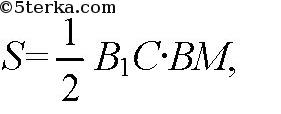
так что

Ну и ОК=ВМ=12 (см). Ответ: 12 см.