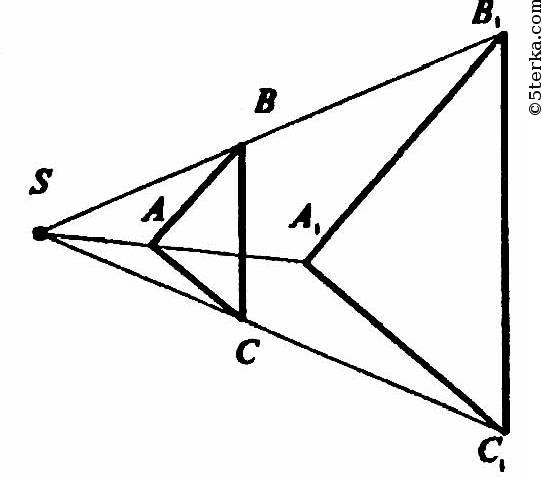
28. Докажите, что преобразование гомотетии в пространстве является преобразованием подобия.

Пусть S - центр гомотетии, тогда

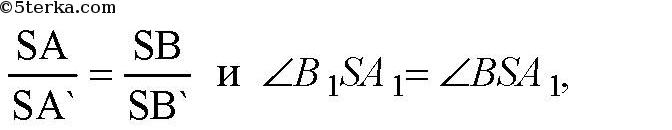
так что ΔSAB~ΔSA₁В₁, значит

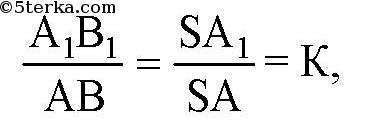
аналогично,

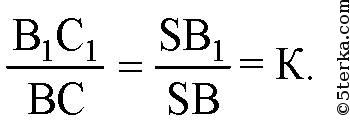
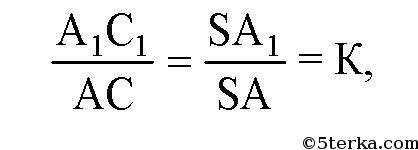
где К - коэффициент гомотетии.

Следовательно,

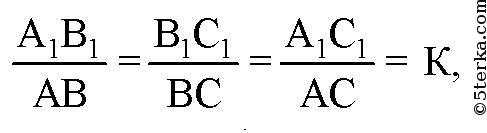
и по третьему признаку ΔАВС ~А₁В₁С₁, то есть преобразование гомотетии в пространстве является преобразованием подобия. Что и требовалось доказать.

Источник:

Решебник по геометрии за 10 класс (А.В. Погорелов, 2001 год),
задача №28
к главе «§18. Декартовы координаты и векторы в пространстве».

Все задачи

← 27. Четыре параллельные прямые пересекают параллельные плоскости в вершинах параллелограммов ABCD и A1B1C1D1 соответственно. Докажите, что параллелограммы ABCD и A1B1C1D1 совмещаются параллельным переносом.

29. Три прямые, проходящие через точку S, пересекают данную плоскость в точках А, В, С, а параллельную ей плоскость в точках А1, В1, С1. Докажите, что треугольники АВС и А1В1С1 гомотетичны. →

Комментарии