6. Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершины треугольника.

Пусть АВС — данный треугольник, О — центр описанной около треугольника окружности, Х — любая точка на перпендикулярной ΔАВС прямой.

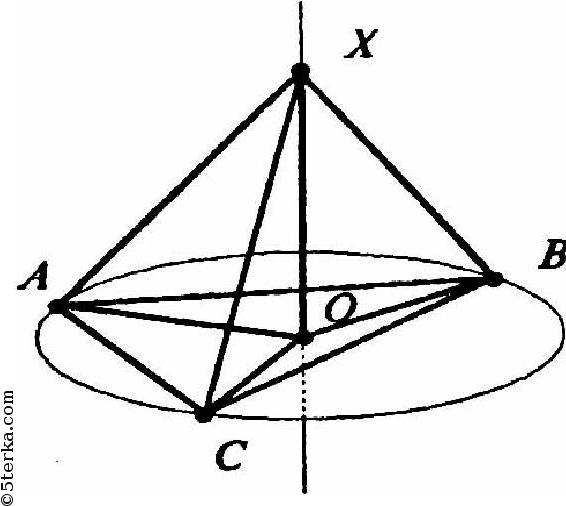
Тогда поскольку О - центр описанной окружности, то ОА = ОВ = =ОС = R. Тогда XA = XB = XC - как наклонные с равными проекциями. Что и требовалось доказать.