30. Три прямые, проходящие через одну точку, пересекают данную плоскость в точках А, В, С, а параллельную ей плоскость в точках А1, В1, С1. Докажите подобие треугольников АВС и А1В1С1.

Пусть О — данная точка.

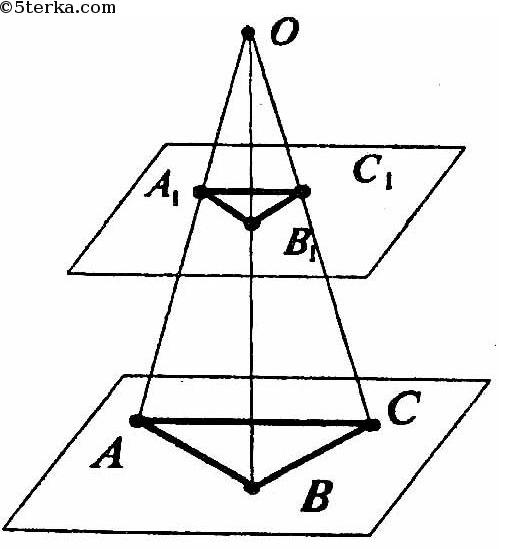
Рассмотрим пары треугольников ОА₁В₁ и ОАВ, ОВ₁С₁ и ОВС, ОС₁А₁ и ОСА.

Так как плоскости α и β параллельны, то эти треугольники подобны.

Из подобия следует, что:

Из этих пропорций получаем, что

А значит, по признаку подобия треугольников (по трем сторонам): ΔАВС~ΔА₁В₁С₁. Что и требовалось доказать.