8. Даны параллелограмм и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках А1, В1, С1 и D1. Найдите длину отрезка DD1, если: 1) АА1 = 2 м, ВВ1 = 3 м, СС1 = 8 м; 2) АА1

Пусть М — точка пересечения диагоналей параллелограмма ABCD. Проведем через М прямую, параллельную прямым АА1, BB1, CC1 и DD1.

Она пересечет данную плоскость в точке М1, так как если одна прямая пересекает плоскость, то и параллельная ей прямая пересекает плоскость. Пусть DD1 = х. MM1 - средняя линия трапеции ACC1A1, (следует из задачи 5). Но с другой стороны MM1 - средняя

линия трапеции DD1B1B. Так что ММ1 = 1/2 (ВВ1 + DD1). Тогда

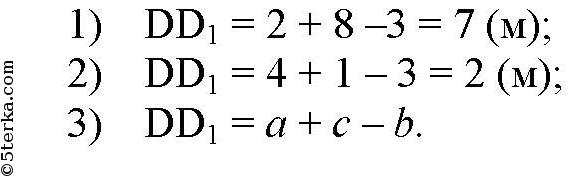
Источник:

Домашняя работа по геометрии за 10 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов Решебник по геометрии за 10 класс (А.В. Погорелов, 2001 год),
задача №8
к главе «§ 16. Параллельность прямых и плоскостей».

Все задачи

← 7. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1 Найдите длину отрезка ВВ1 если:1) СС1 = 15см, АС : ВС = 2 : 3;2) СС1 = 8,1см, АВ : АС = 1
9. Прямые а и b не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и b? →
Комментарии