№ 62*. Докажите, что если sin a = sin b, то либо a = b, либо a = 180° - b.

Пусть

точки пересечения окружности с центром (0; 0) радиуса R со стороной угла a и в соответственно, отложенных от положительной полуоси х в верхнюю полуплоскость, где у>0. По определению

Поскольку точки А и В лежат на окружности с центром (0; 0) радиуса R, то

и

но

так как

Так как

Значит, либо

либо

Если

то

совпадают и

если

то опустим перпендикуляры

из

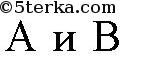
на ось х. Тогда

Поэтому

(по трем сторонам), значит,

является смежным с углом

значит,

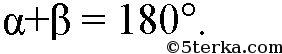
То есть

Что и требовалось доказать.