№ 31*. На прямолинейном шоссе требуется указать место автобусной остановки так, чтобы сумма расстояний от нее до населенных пунктов А и В была наименьшей. Рассмотрите два случая: 1) населенные пункты расположены по разные стороны от шоссе; 2) населенные п

№ 31*. На прямолинейном шоссе требуется указать место автобусной остановки так, чтобы сумма расстояний от нее до населенных пунктов А и В была наименьшей. Рассмотрите два случая: 1) населенные пункты расположены по разные стороны от шоссе; 2) населенные пункты расположены по одну сторону от шоссе. 1)

Обозначим шоссе а.

Если А и В лежат по разные стороны от а, то остановка О

должна быть в точке пересечения отрезка АВ с а. Если

не лежит на АВ, то по неравенству треугольника в

сумма двух сторон треугольника больше третьей стороны; то есть

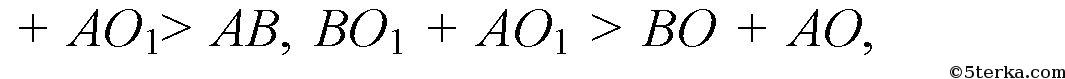
значит,

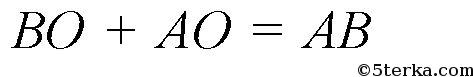
наименьшая сумма расстояний от остановки О до населенных пунктов А и В. И точка О - искомая. 2)

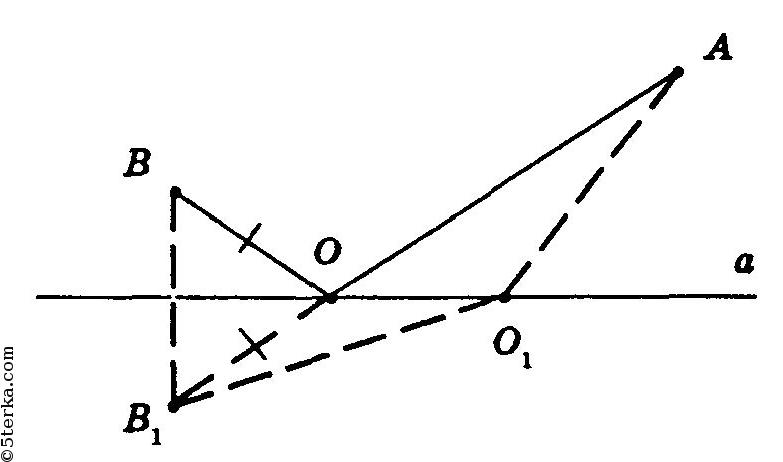
Построим точку

симметричную

относительно прямой а. Пусть точка О — точка пересечения

Тогда сумма расстояний

будет наименьшей. Так как

то и сумма расстояний

тоже будет наименьшей и