№ 38. Постройте ромб: 1) по углу и диагонали, исходящей из вершины этого угла; 2) по диагонали и противолежащему углу.

1) Строим данный угол и проводим биссектрису. От вершины биссектрисы откладываем диагональ АВ и делим ее пополам, точкой О. Проводим перпендикуляр через точку О к диагонали АВ, который пересекает стороны угла в точках С и D, которые являются вершинами искомого ромба.

2) Пусть дан угол а и диагональ d. Необходимо построить ромб, в котором один из углов равен а, а противолежащая диагональ равна d.

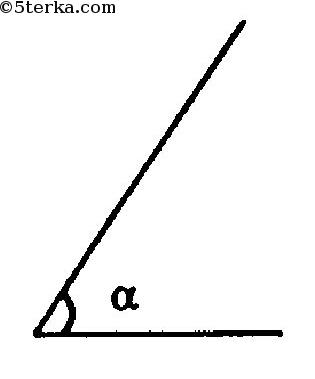
Предположим, что существует ромб ABCD, в котором диагональ

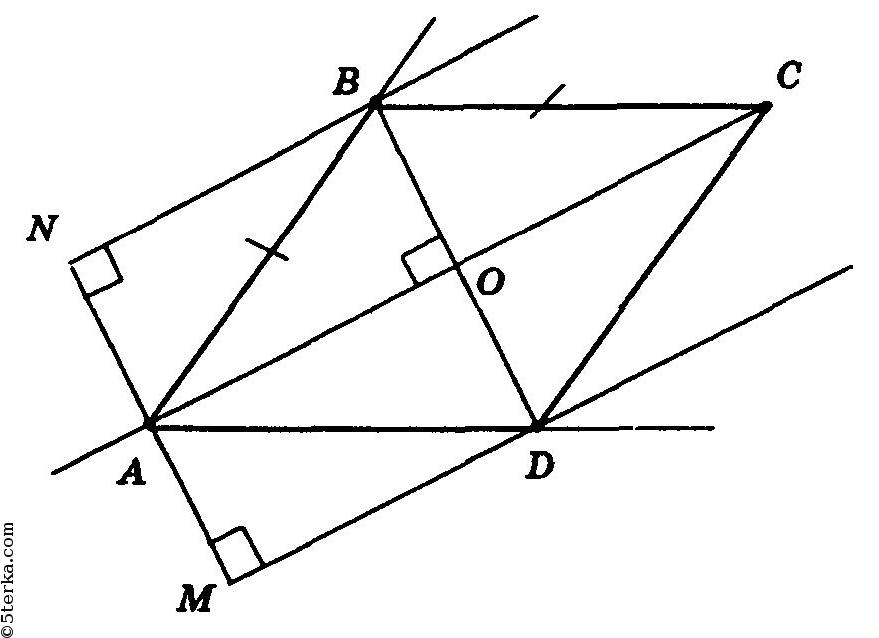
Диагональ АС — биссектриса

Проведем через точку A прямую

и отложим отрезки

по разные стороны от точки А, следовательно,

прямоугольник. Построим

Проведем биссектрису AC угла BAD.

Через точку А проведем прямую

и от точки А отложим

Проведем через

прямые, параллельные АС, точки пересечения этих прямых со сторонами угла BAD обозначим соответственно В и D. Раствором циркуля, равным АВ, проведем дугу с центром В, при этом, точку пересечения дуги с прямой а обозначим С. Получим четырехугольник ABCD. Докажем, что ABCD — ромб в котором

— по построению. Так как 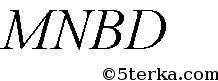прямоугольник по построению, то отрезок АО — серединный перпендикуляр к BD и

равнобедренный

ОС серединный перпендикуляр в

значит,

— равнобедренный

Так как

по построению, то

и

ромб с

По построению

значит,

искомый ромб.