№ 17. В параллелограмме ABCD точка Е — середина стороны ВС, а F — середина стороны AD. Докажите, что четырехугольник BEDF — параллелограмм.

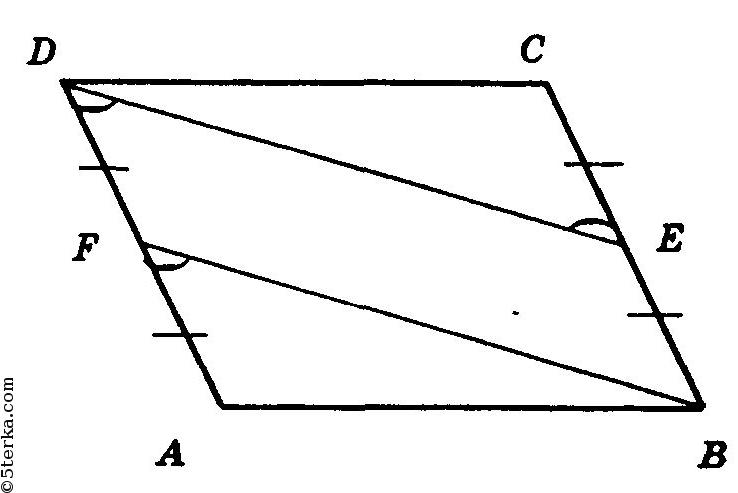
Докажем, что 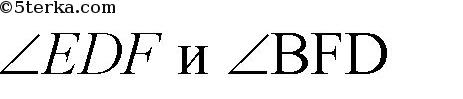— односторонние для прямых 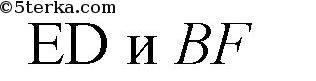и секущей 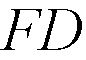и их сумма равна 180°, а значит, прямая и, тогда, четырехугольник — параллелограмм. Рассмотрим

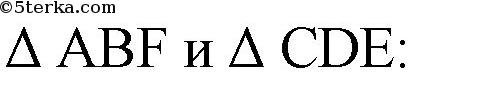
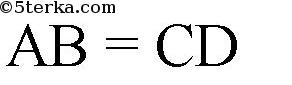— противоположные стороны параллелограмма.

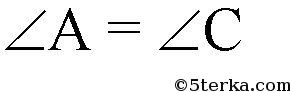— противоположные углы параллелограмма.

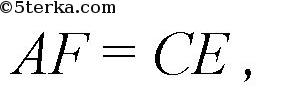
так как

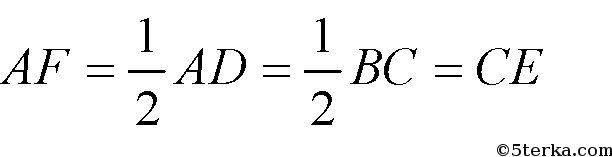
Значит,

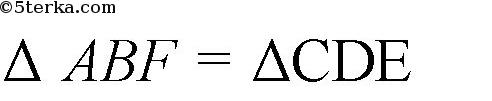— по двум сторонам и углу между ними. Следовательно

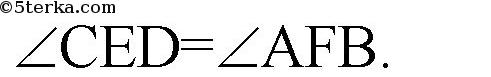
Но

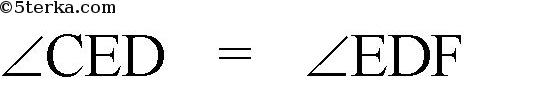
(накрест лежащие для параллельных 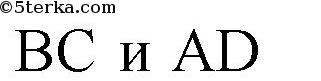и секущей 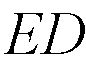). Значит

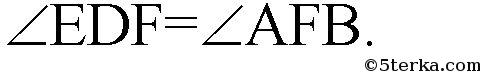
Поэтому

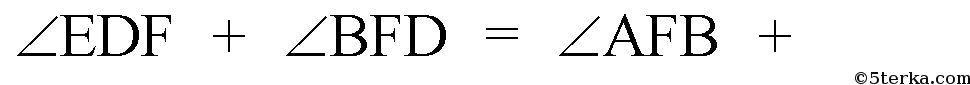
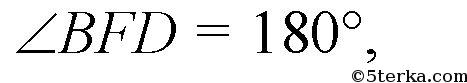
так как

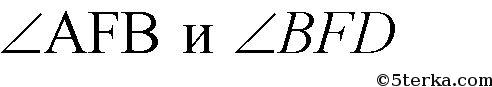— смежные углы. Тогда, и четырехугольник параллелограмм. Что и требовалось доказать.