18.23. а) Точки (0; 0), (2; 0), (3; 2) являются вершинами треугольника. Сколькими способами можно обозначить эти вершины буквами А, В, С? б) Точки (0; 0), (0; 4), (3; 0), (3; 7) являются вершинами трапеции. Сколькими способами можно обозначить эти вершины

18.23. а) Точки (0; 0), (2; 0), (3; 2) являются вершинами треугольника. Сколькими способами можно обозначить эти вершины буквами А, В, С? б) Точки (0; 0), (0; 4), (3; 0), (3; 7) являются вершинами трапеции. Сколькими способами можно обозначить эти вершины буквами К, L, М, N? в) Точки (1; -3), (0; 0), (0; 4), (3; 0), (3; 7) являются вершинами выпуклого пятиугольника. Сколькими способами можно обозначить эти вершины буквами Р, R, S, Т, Q? г) В скольких случаях в задании в) PR будет одной из сторон?

18.23.

а)

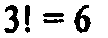
б)

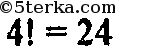
в)

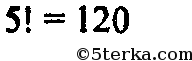
г) 10 способами мы можем выбрать точки Р и R так, чтобы PR была одной стороной. При фиксированных Р и R, остальные точки выбираются 3! = 6 способами. Всего 10*6 = 60.

Источник:

Решебник по алгебре за 9 класс (А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина и др., 2010 год),
задача №18.23.
к главе «§18. Комбинаторные задачи».

Все задачи

← 18.22. Известно, что х = 2^a3^b5^c и a, b, c — различные числа из множества {0, 1, 2, 3}. а) Найдите наименьшее и наибольшее значения числа х. б) Сколько всего таких чисел можно составить? в) Сколько среди них будет нечетных

18.24. В волейбольной команде шесть человек, а на площадке шесть позиций (номеров) для их расстановки. а) Сколькими способами команда может расположиться на площадке? б) Сколько есть способов расположения, при которых капитан находится на подаче? в) Сколь →

Комментарии