839 Середины К и М сторон АВ и DC выпуклого четырехугольника ABCD соединены отрезками KD, КС, МА и MB с вершинами. Докажите, что площадь четырехугольника, заключенного между этими отрезками, равна сумме площадей двух треугольников, прилежащих к сторонам AD и ВС.
Решение.
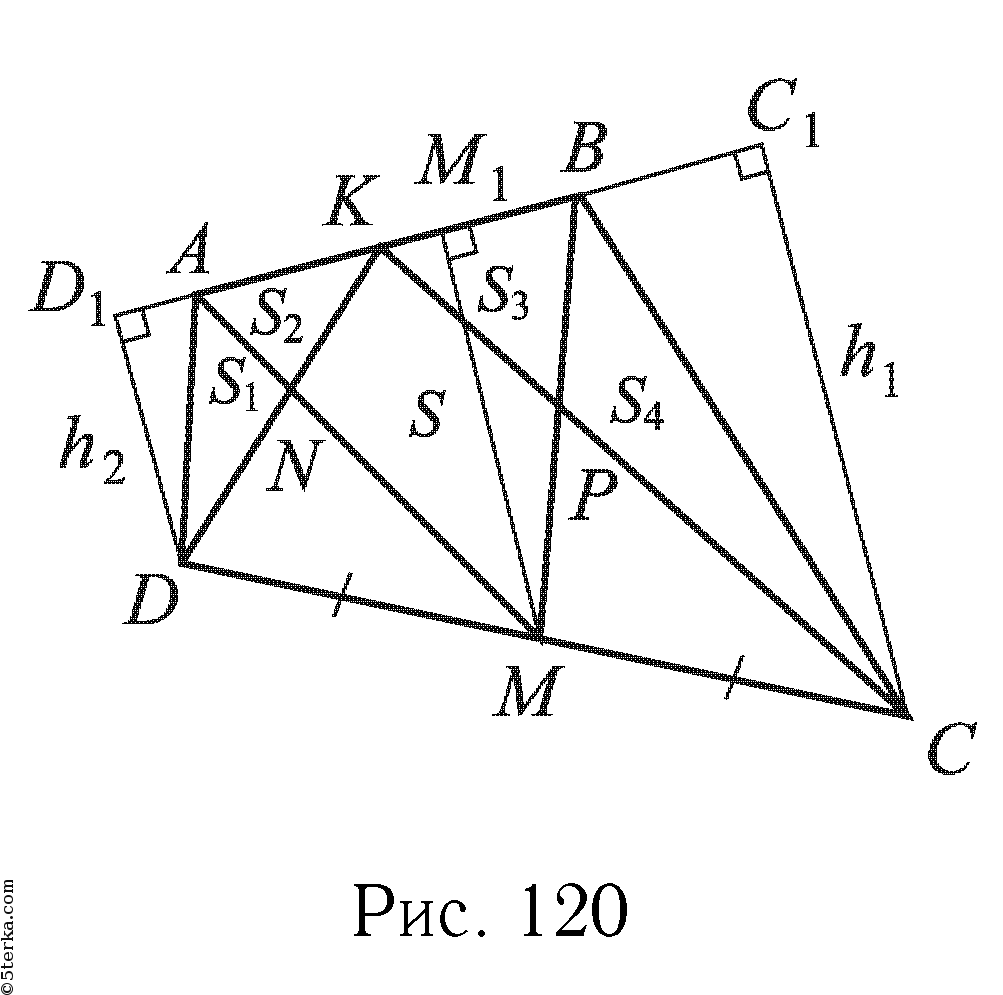
На рисунке 120 изображена данная фигура, N и Р — точки пересечения отрезков DK и AM, КС и ВМ. Требуется доказать, что
Источник:
Решебник
по
геометрии
за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №839
к главе «Глава VI. Площадь. Задачи повышенной трудности».
Комментарии