391 Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости.

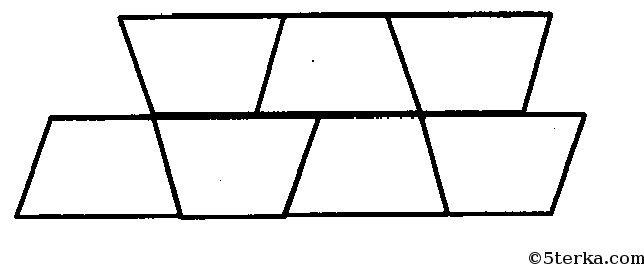
Решение #1.

Условие задачи сформулировано некорректно. Доказательство невозможно.

Пример! Пусть S - площадь паркетной плитки в виде равнобедренной трапеции, S₁ - некая площадь, ограниченная стенами. Тогда при S>S₁ паркет уложить нельзя.

Решение #2.

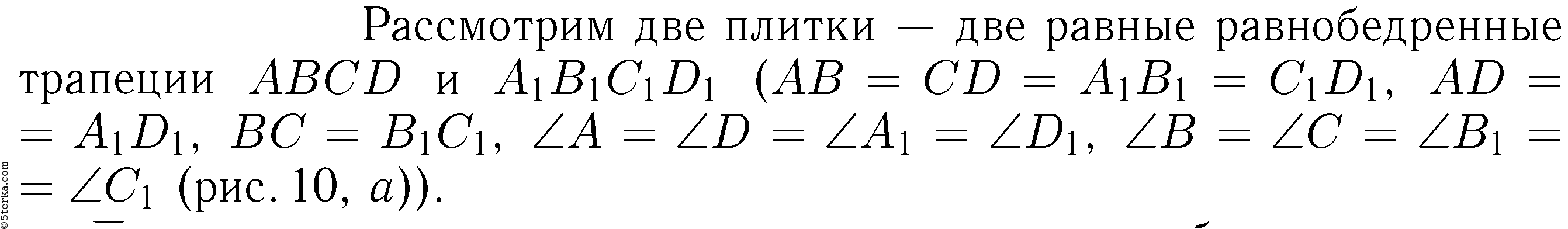
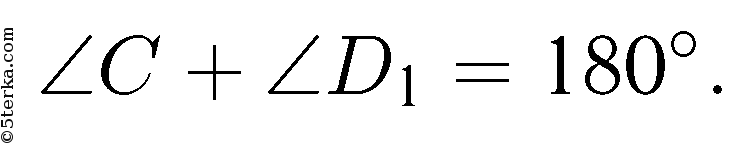
Следовательно, можно построить 3 параллелограмма, удовлетворяющие данному условию.