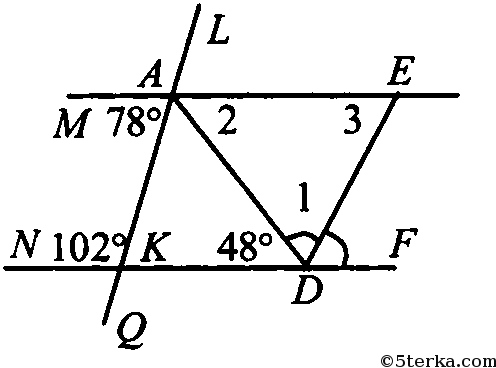
∠МАК и ∠NKA - односторонние при прямых ME и NF и секущей АК и ∠МАК + ∠NKA = 78° + 102° = 180°, следовательно ME || NF (по признаку параллельности прямых).
∠KDA и ∠ADF- смежные, тогда ∠KDA + ∠ADF= 180°;
48° + ∠ADF= 180°, т.е ∠ADF= 132°.
Т.к. DE - биссектриса ADF, ∠1 = ∠EDF = 132° : 2 = 66°; т.к. ME || NF, ∠3 = ∠EDF = 66° (накрест лежащие).
∠1 + ∠2 + ∠3 = 180° (сумма углов треугольника) или 66° + ∠2 + 66° = 180°, значит ∠2 = 48°.
Источник:
Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №216
к главе «Глава III. Параллельные прямые. §2 Аксиома параллельных прямых».
Комментарии