695. Найдите объем треугольной пирамиды SABC, если: а) ∠САВ = 90°, ВС = с, ∠АВС=φ и каждое боковое ребро составляет с плоскостью основания угол Θ; б) АВ= 12 см, ВС = CA = 10 см и двугранные углы при основании равны 45°; в) боковые ребра

695. Найдите объем треугольной пирамиды SABC, если: а) ∠САВ = 90°, ВС = с, ∠АВС=φ и каждое боковое ребро составляет с плоскостью основания угол Θ; б) АВ= 12 см, ВС = CA = 10 см и двугранные углы при основании равны 45°; в) боковые ребра попарно перпендикулярны и имеют длины а, b и с.

а) Построим высоту DE, отрезки ЕА, ЕВ, ЕС.

Тогда

R — радиус окружности, описанной около ΔАВС. Значит, точка Е является серединой ВС,

плоскость CDB ⊥ плоскости АВС;

Из треугольника DEB:

В треугольнике АВС:

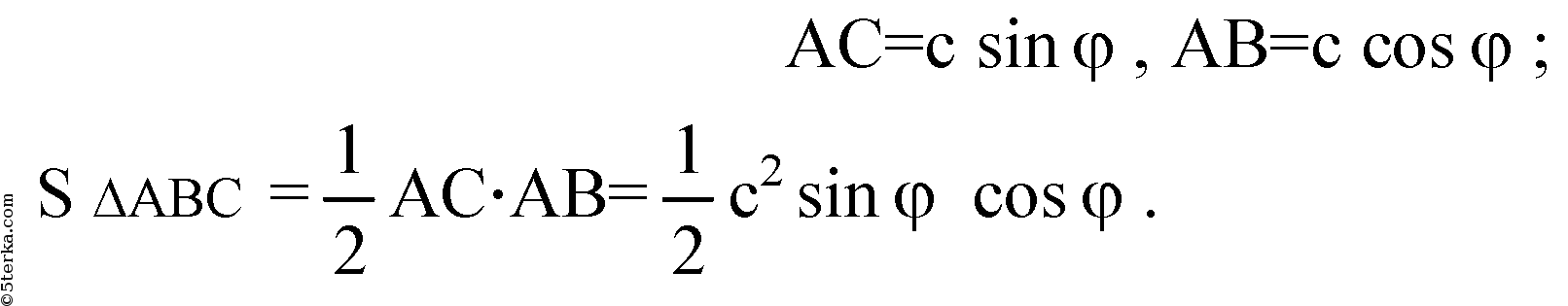
б) Проведем

По теореме о трех перпендикулярах имеем

Тогда,

r — радиус вписанной в ΔАВС окружности.

Из ΔDOL:

в)

AS перпендикулярна плоскости BSC, AS — высота пирамиды.