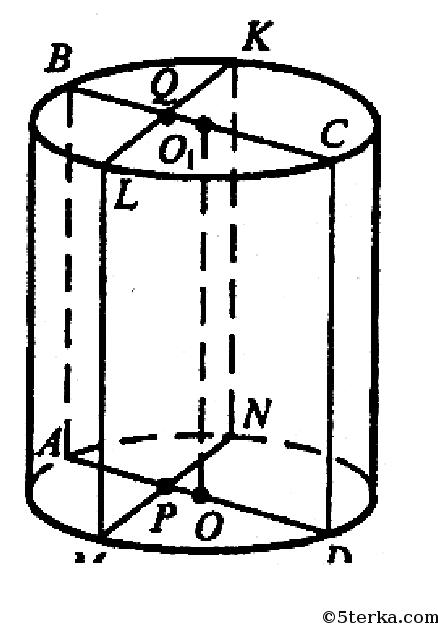
Осевое сечение ABCD и сечение MNKL являются прямоугольниками. Пусть образующая цилиндра LM= l, следовательно,
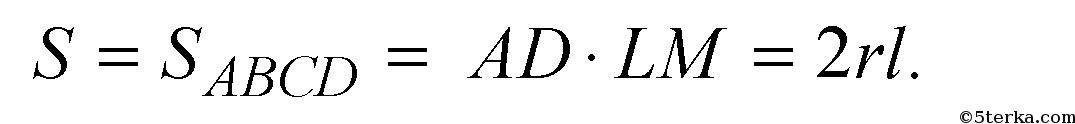
Выразим длину отрезка MN.

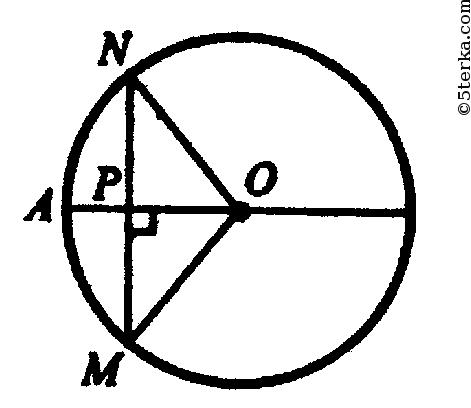
Из прямоугольного треугольника ONP найдем:
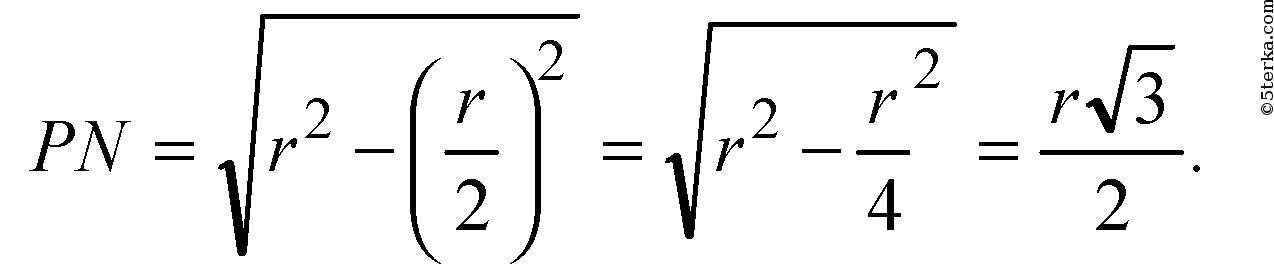
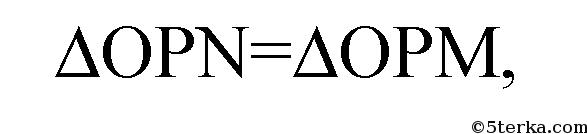
следовательно, NP=PM,
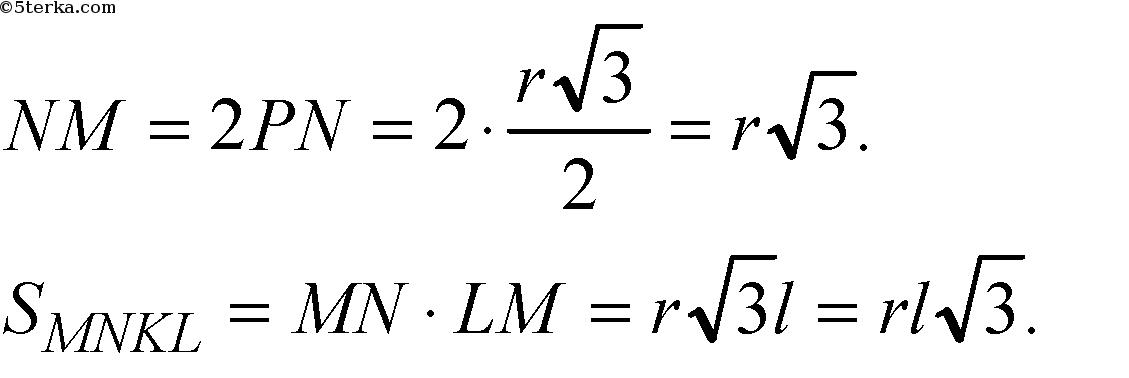
Итак,

отсюда
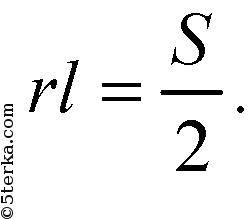
Поэтому
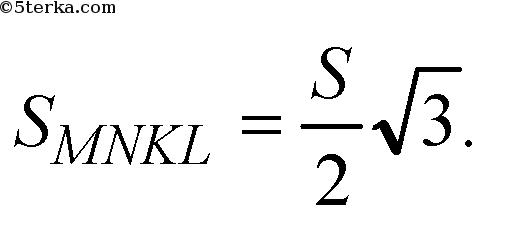
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №601
к главе «Глава VI. Цилиндр, конус и шар. Дополнительные задачи».
Комментарии