528. Докажите, что если секущая плоскость параллельна оси цилиндра и расстояние между этой плоскостью и осью цилиндра меньше его радиуса, то сечение цилиндра представляет собой прямоугольник, две противоположные стороны которого — образующие цилиндра.
Пусть π — секущая плоскость, π|| O1O.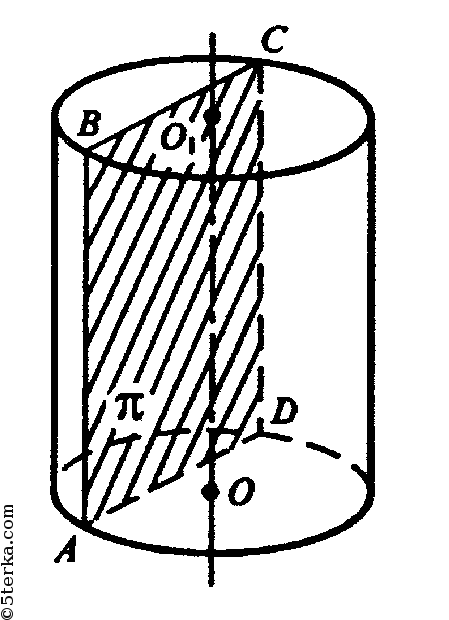
O1O ⊥ плоскостям оснований, тогда прямые АВ и CD, по
которым п пересечет боковую поверхность цилиндра, также перпендикулярны плоскостям оснований. Тогда АВСD — прямоугольник. Точка А переходит в точку В и точка D переходит в точку С.
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №528
к главе «Глава VI. Цилиндр, конус и шар § 1. цилиндр».
Комментарии