246. Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведенная из вершины пирамиды, равна 41 см. а) Докажите, что высота пирамиды проходит через центр окружности, вписанной в ее основание; б) Найдите площадь основания пирамиды, е

246. Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведенная из вершины пирамиды, равна 41 см. а) Докажите, что высота пирамиды проходит через центр окружности, вписанной в ее основание; б) Найдите площадь основания пирамиды, если его периметр равен 42 см.

а) Пусть высота пирамиды — РО, а высоты боковых граней РА1, РВ1, РС1 (рис. 161 ).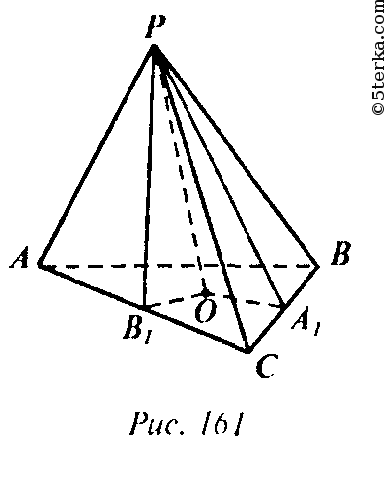

ОА1 — проекция РА1, поэтому ОА1 ⊥ ВС. Значит OA1 — расстояние от точки О до BC. Аналогично ОВ1 и ОС1 — расстояние от точки О до АС и AB соответственно. Но по теореме Пифагора:

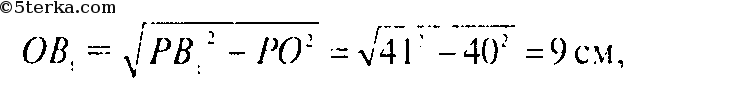
аналогично ОА1 и ОС1 равны 9 см. Но это и означает, что О — центр вписанной окружности. б) Площадь треугольника S вычисляется через радиус r вписанной окружности и полупериметр p последующей формуле:

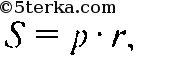
поэтому

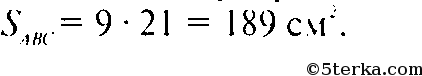
Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №246
к главе «Глава III Многогранники. § 2. Пирамида».

Все задачи

← 245. Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30° и 45°. Найдите площадь поверхности пирамиды.
247. Двугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых граней, проведенные из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды рав →
Комментарии