1) Три равные окружности касаются друг друга. OЕ = R.
Проведем SD ⊥ OЕ и MN ⊥ OЕ, тогда, SD || MN.
Рассмотрим ΔOMD и ΔOEN: ∠M = ∠Е (как прямые); ∠N = ∠D (соответственные). Тогда, ΔOMD ~ Δ0EN.
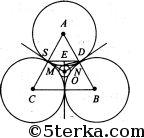
2) Пусть четыре равные окружности, касаются друг друга, и окружность с центром в точке О и радиусом ОЕ = R.
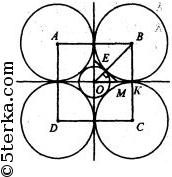
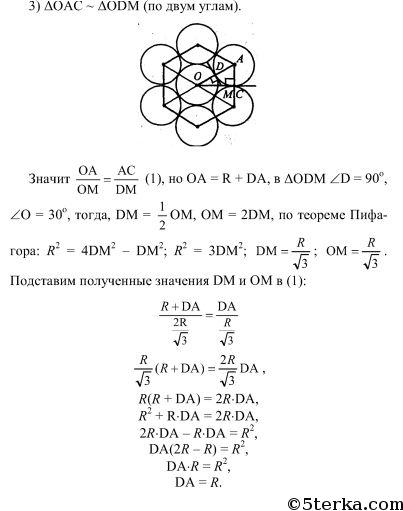
Источник:
Решебник
по
геометрии
за 9 класс (А.В.Погорелов, 2001 год),
задача №41
к главе «§13. Многоугольники».
Комментарии