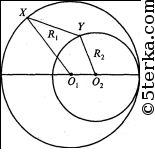
№ 2. Решите задачу 1 при условии, что G < R1 - R2.


Пусть X и Y — точки на окружностях. По теореме о длине ломаной для ломаной XO1O2Y имеем:

XY  ≤ XO1 + O1O2 + O2Y,

то есть ХO1 + O1O2 + O2Y = R1 + R2+ d — наибольшее расстояние.

Для ломаной XYO2O 1 имеем:

XO1 ≤ XY + YO2 + O1O2; R1 ≤ XY +R2+d, XY ≥ R1 - R2 - d,

значит, (R1 - R2 - d) — наименьшее расстояние.

Источник:

Домашняя работа по геометрии за 9 класс к учебнику «Геометрия. 7-9 класс» А.В.Погорелов Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №2
к главе «§13. Многоугольники».

Все задачи

← № 1. Даны две окружности с радиусами R1 и R2 и расстояние между центрами d > R1 + R2. Чему равны наибольшее и наименьшее расстояния между точками X и Y этих окружностей.
№ 3. Докажите, что если вершины ломаной не лежат на одной прямой, то длина ломаной больше длины отрезка, соединяющего ее концы. →
Комментарии