№ 24. В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ. На ней взята точка D. Докажите равенство треугольников: 1) ABD и CBD; 2) AMD и CMD.

Т.к. ВМ — медиана равнобедренного треугольника, то она является и высотой и биссектрисой. Таким образом, ∠AMD = ∠DMC = 90°, ∠ABD = ∠DBC,

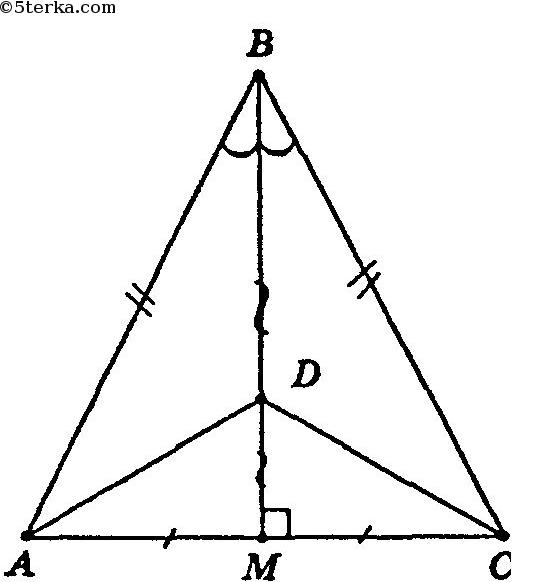
1) В ΔABD и ΔDBC: АВ = ВС (т.к. ΔАВС равнобедренный), BD — общая.

∠ABD = ∠DBC (т.к. ВМ — биссектриса). Таким образом, ΔABD = ΔDBC по 1-му признаку равенства треугольников.

2) В ΔADM и ΔMDC:

АМ = МС (т.к. ВМ — медиана)

DM — общая ∠AMD = ∠DMC = 90^о Таким образом, ΔADM = ΔMDC по 2-м катетам, что и требовалось доказать.