Проведем ось SS1, которая перпендикулярна плоскости ABCD. Так как верхняя часть октаэдра — правильная пирамида, то О — центр окружности, вписанной в квадрат ABCD.
Обозначим ребро октаэдра х. Тогда
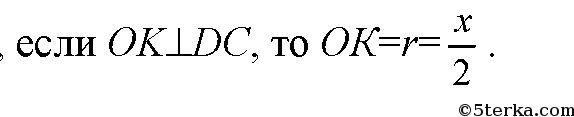
Проведем SК и S1K, тогда по теореме о трех перпендикулярах имеем SK⊥DC и S1K⊥DC. Так что ∠SKS1 — линейный угол искомого двугранного угла.
Из правильного ΔSDC:
, а из ΔS1DC:
Далее, из прямоугольного δSOK по теореме Пифагора получаем:
Так что
По теореме косинусов в ΔSKS1:
Так что,
Тогда
Остальные двугранные углы равны найденному.
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №82
к главе «§ 20. Многогранники».
Комментарии