№ 51*. При каких значениях с прямая х + у + с = 0 и окружность х2 + у2 = 1: 1) пересекаются; 2) не пересекаются; 3) касаются?

Координаты точек пересечения являются решением системы уравнений:

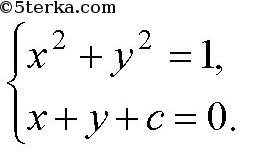
Окружность и прямая пересекаются, если система имеет решения. 1)

2)

Система будет иметь решения, если квадратное уравнение имеет корни, то есть, если

будет неотрицательным,

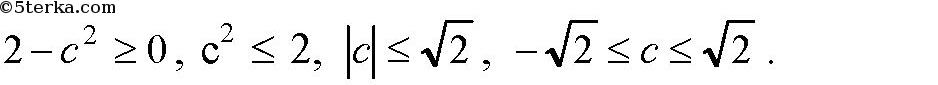
То есть при

уравнение (2) имеет два корня, а значит, система имеет два решения, окружность и прямая пересекаются в двух различных точках; при

или

уравнение (2) имеет один корень, система имеет одно решение, значит, окружность и прямая касаются. А при

или

система не имеет решений, так как уравнение (2) не имеет решений, значит, окружность и прямая не пересекаются. Ответ: 1) пересекаются, если

2) не пересекаются, если

или

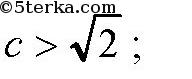
3) касаются, если

или