№ 20. Докажите, что расстояние между любыми двумя точками на сторонах треугольника не больше большей из его сторон.

Пусть в

— большая сторона,

Рассмотрим

Согласно результату задачи

можно утверждать, что

или

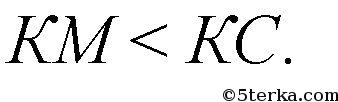
Если

то

а значит и

но так как АС — большая сторона, то АВ < АС, значит и КМ < АС. Если КМ < КС, то согласно задаче № 19 для ААВС можно утверждать, что КС < ВС или КС < АС, но так как АС — большая сторона, то КС < АС, а значит, и КМ < АС. Так что КМ < АС в любом случае. Что и требовалось доказать.

Источник:

Решебник по геометрии за 8 класс (А.В. Погорелов, 2001 год),
задача №20
к главе «§ 7. Теорема Пифагора».

Все задачи

← № 19. На стороне АВ треугольника АВС взята точка X. Докажите, что отрезок СХ меньше по крайней мере одной из сторон АС или ВС.

№ 21. Даны прямая и точка С на расстоянии h от этой прямой. Докажите, что из точки С можно провести две и только две наклонные длины l, если l > h. →

Комментарии