№ 49. Отрезок ВС пересекает прямую а в точке О. Расстояния от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС.

В ΔОВВ₁ и ΔОСС₁:

∠ВОВ₁ = ∠СОС₁ (как вертикальные),

∠В₁ = ∠С₁ = 90°

∠В = 90° - ∠ВОВ₁ = 90° - ∠С₁ОС = АС ОВ = ОС (из условия)

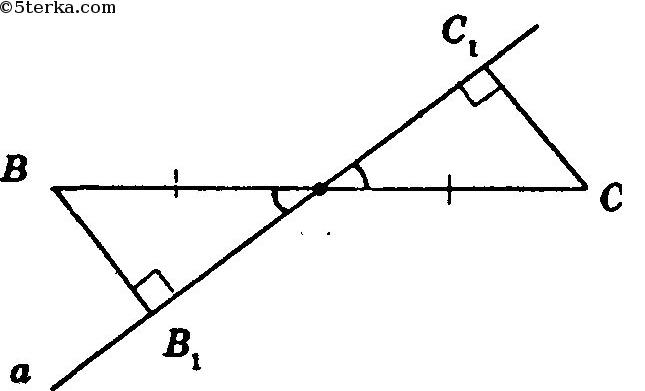
Таким образом, ΔОВВ₁ = ΔОСС₁ по 2-му признаку равенства треугольников, откуда ОВ = ОС. Таким образом, точка О — середина отрезка ВС.