334 Через каждую вершину данного треугольника проведена прямая, перпендикулярная к биссектрисе треугольника, исходящей из этой вершины. Отрезки этих прямых вместе со сторонами данного треугольника образуют три треугольника. Докажите, что углы этих треугольников соответственно равны.

Пусть дан ΔАВС, а прямые, перпендикулярные к биссектрисам треугольника пересекаются в точках Р, Q и R. AM1, ВМ2 и CM3 - биссектрисы ΔАВС
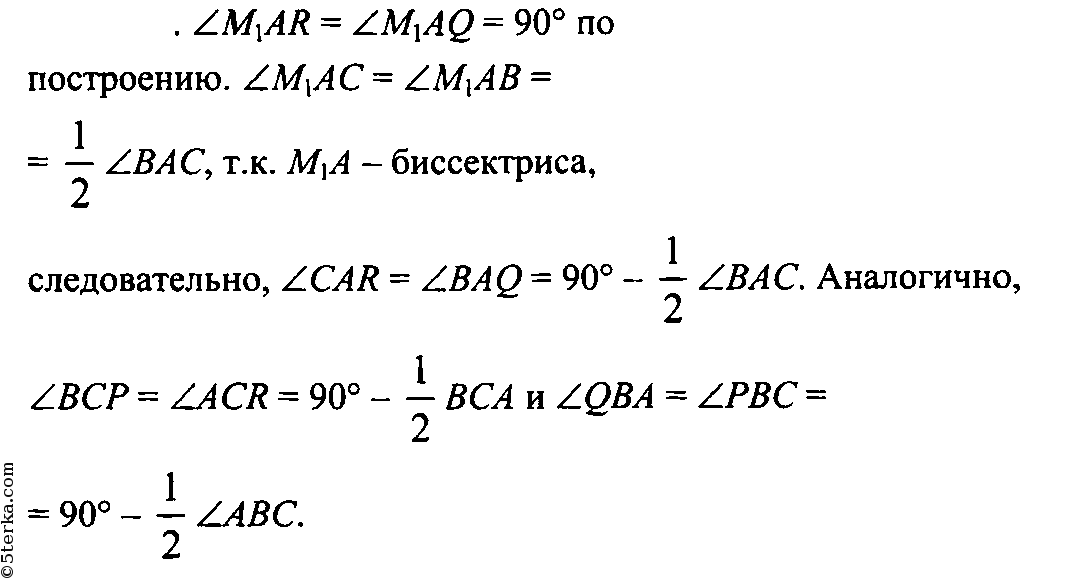
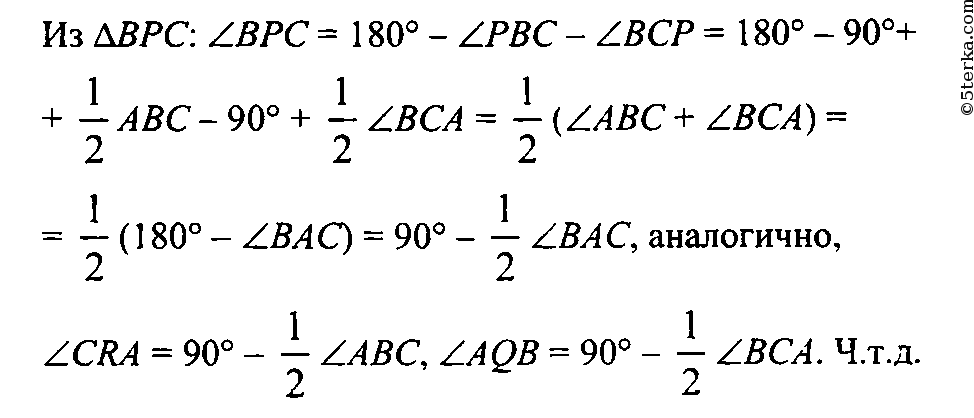
Источник:
 Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №334
к главе «Задачи повышенной трудности. Задачи к главам III и IV».
Комментарии