Решение
Даны отрезки P1Q1 и P2Q2 и угол hk (рис. 144, а). Требуется построить треугольник ABC, у которого одна из сторон, скажем АВ, равна отрезку P1Q1, один из
прилежащих к ней углов, например угол А, равен данному углу hk, а высота СН, проведенная к стороне АВ, равна данному отрезку P2Q2.
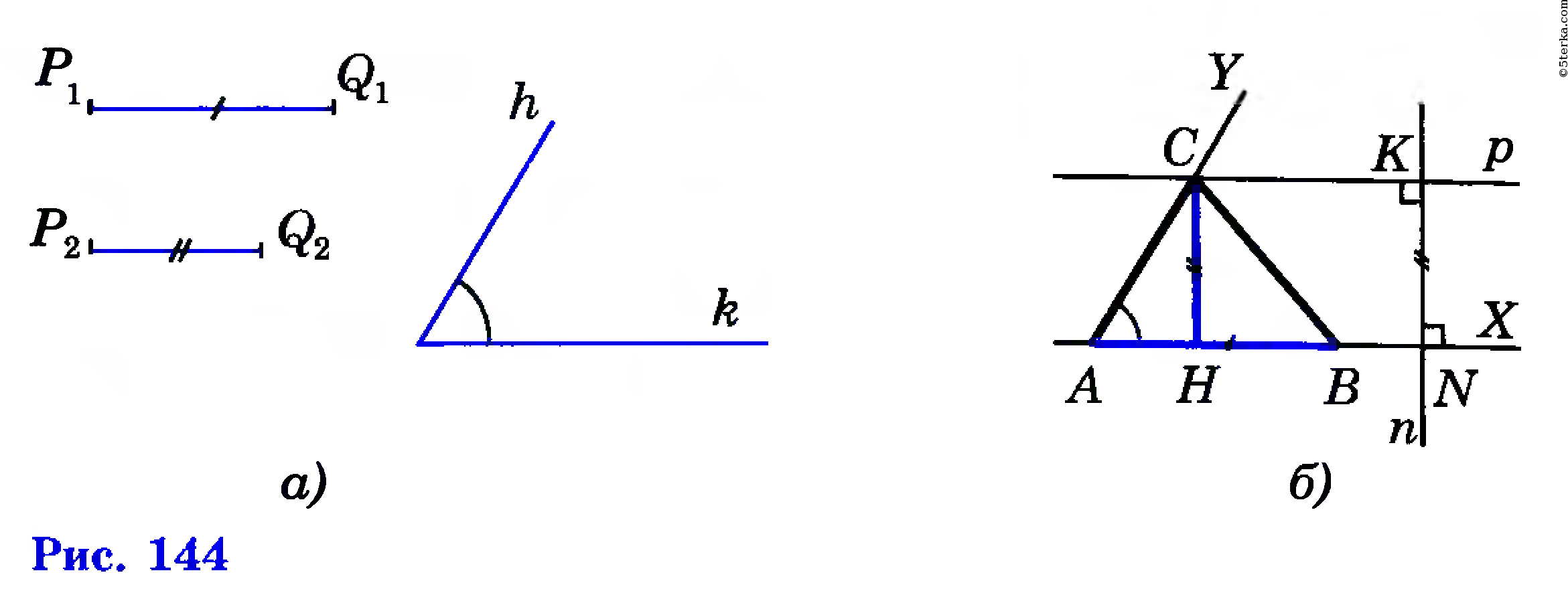
Построим угол XAY, равный данному углу hk, и отложим на луче АХ отрезок AB, равный данному отрезку P1Q1 (рис. 144, б). Для построения вершины С искомого треугольника заметим, что расстояние от точки С до прямой AB должно равняться P2Q2. Поэтому точка С должна лежать на прямой р, параллельной прямой AB и такой, что расстояние между прямыми р и AB равно P2Q2. Следовательно, искомая точка С есть точка пересечения прямой р и луча AY.
Построение прямой р описано в решении задачи 284. Очевидно, треугольник ABC удовлетворяет всем условиям задачи: AB=P1Q1, CH=P2Q2, ∠A=∠hk.
 Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №293
к главе «Глава IV. Соотношения между сторонами и углами треугольника. §4 Построение треугольника по трем элементам».