№ 41. Докажите, что геометрическое место точек, удаленных от данной прямой на расстояние h, состоит из двух прямых, параллельных данной и отстоящих от нее на h.

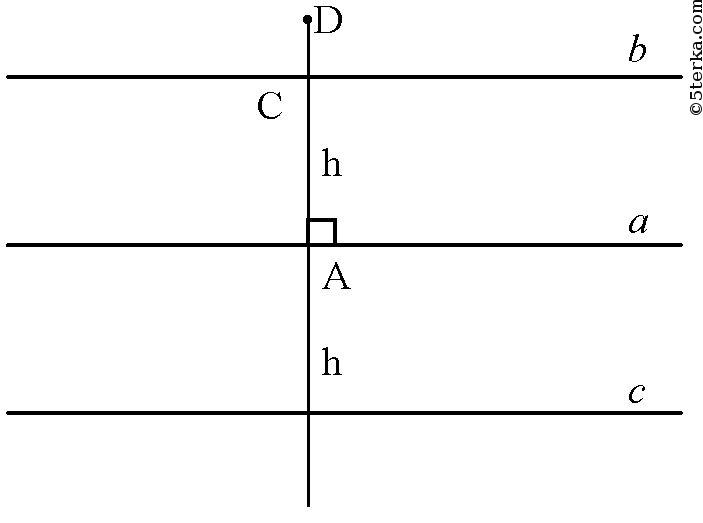
Т.к. расстояние от прямой до некоторой точки — это есть перпендикуляр к этой прямой через эту точку

Докажем, что любая точка, удаленная от а на h лежит либо на с, либо на b.

Пусть точка D не лежит ни на b, ни на с, и расстояние от D до точки А на прямой равно h.

Тогда DA = h и AD ⊥ a.

Но СА также равно h и СА ⊥ а.

Следовательно, точки С и D либо совпадают, либо противоположны относительно прямой а.

То есть точка D лежит на прямой b или на с.