Исследование равноускоренного движения без начальной скорости.
Задание 1. Убедитесь в том, что брусок движется по наклонной плоскости равноускоренно.
Задание 2. Определите ускорение движения бруска.
Задание 3. Определите мгновенную скорость движения бруска в разные моменты времени и постройте график зависимости мгновенной скорости от времени.
Задание 4. Постройте график зависимости координаты х бруска от времени t, отсчитываемого от начала движения.
Вариант 1.
Цель работы: определить ускорение движения шарика и его мгновенную скорость перед ударом о цилиндр.
Движение шарика по наклонному желобу является равноускоренным. Если мы отпустим без начальной скорости шарик и измерим пройденное им расстояние s до столкновения с цилиндром и время t от начала движения до столкновения, то мы можем рассчитать его ускорение по формуле:

Зная ускорение а, мы можем определить мгновенную скорость v по формуле:

Пример выполнения работы.
 |  |  |  |  |
|
3 |
0,9 |
1,5 |
0,8 |
1,2 |
Вычисления.

Вариант 2.
Цель работы: убедиться в равноускоренном характере движения бруска и определить его ускорение и мгновенную скорость.


Если эта закономерность выполняется для измеренных в работе модулей векторов перемещений, то это и будет доказательством того, что движение бруска по наклонной плоскости является равноускоренным.
Пример выполнения работы.
Задание 1. Исследование характера движения бруска по наклонной плоскости.
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
Вычисления.

Отсюда находим:

Эта закономерность не очень сильно отличается от теоретической закономерности для равноускоренного движения. Таким образом, можно считать, что движение бруска по наклонной плоскости является равноускоренным.
Задание 2. Определение ускорения движения бруска.
Ускорение будем вычислять по формуле:



Задание 3. Определение мгновенной скорости бруска в разные моменты времени и построение графика зависимости мгновенной скорости v от времени t.
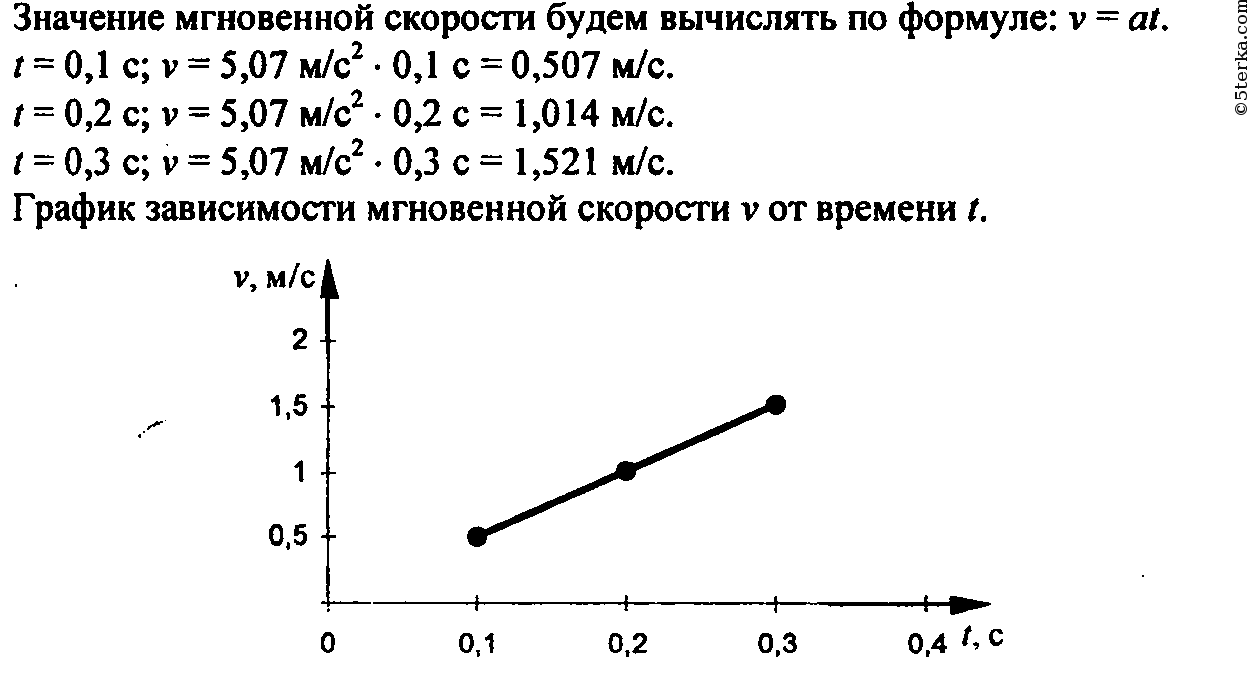
Задание 4. Построение графика зависимости координаты х бруска от времени t.

 Решебник
по
физике
за 9 класс (А.В.Перышкин, Е.М.Гутник, 2009 год),
Решебник
по
физике
за 9 класс (А.В.Перышкин, Е.М.Гутник, 2009 год),
задача №1
к главе «Лабораторные работы».