Механические колебания и волны к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Говорят, что некая физическая величина x совершает колебания, если зависимость x(t), где t — время, есть периодическая или приближенно периодическая функция. Назовем периодом колебания такое время T, что для всех T имеет место равенство
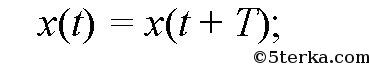
очевидно, что таких T бесконечно много, поэтому мы будем выбирать из всех T минимальное положительное число. Частотой v называется величина, обратная периоду:
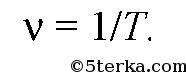
Циклической частотой ω называется частота v, умноженная на 2π:

Колебание называется гармоническим, если x(t) является гармонической функцией

где A называется амплитудой, а φ начальной фазой колебания.
Гармонические колебания совершает груз массой m на пружине жесткости к. Можно доказать, что в этом случае

Также гармонические колебания совершает грузик на нити длины l, если угол отклонения нити от вертикали невелик. Можно доказать, что в этом случае

где g — ускорение свободного падения.
Выше приведены формулы для расчета частот, на которых в отсутствие затухания будет колебаться маятник, когда на него не действуют внешние силы. Такие колебания называются свободными, а эти частоты собственными. Если на колебательную систему, например шарик на пружинке, действует периодическая сила с частотой VB (эта сила называется вынуждающей), то такие колебания называются вынужденными. При вынужденных колебаниях маятник колеблется с частотой vB. Если vB будет равна частоте свободных ко
лебаний v, можно наблюдать явление резонанса. Оно состоит в значительном росте амплитуды колебаний.
Рассмотрим теперь волновое движение. Волна является распространяющимися со скоростью v колебаниями. Пусть v — частота этих колебаний. Назовем длиной волны X расстояние между соседними максимумами. Несложно доказать следующую формулу v=λv.
При нормальных условиях скорость звука, т. е. скорость распространения звуковых волн, в воздухе 330м/с, в воде 1400м/с.