Основы кинематики к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Механическим движением называется изменение положения тела с течением времени. Кинематика, как раздел механики, исследует движение тел, не рассматривая его причин. Одним из самых важных частных случаев механического движения является поступательное движение. При нем любая ось, проведенная через тело, остается параллельной самой себе.
Для удобства описания поступательного движения используется понятие материальной точки. Материальной точкой называется тело, размерами которого при решении данной задачи мы можем пренебречь. Материальная точка — это модель, и в природе их не существует. Не следует забывать, что одно и то же тело в одних условиях можно рассматривать как материальную точку, а в других нельзя. Например, при движении Земли вокруг Солнца Землю можно считать материальной точкой, а при движении пешехода по ней, конечно, нельзя.
Описывая движение, физики используют понятие системы отсчета. Чтобы ввести систему отсчета необходимо задать тело отсчета, систему координат, связанную с этим телом и устройство для измерения времени. Радиус-вектором материальной точки называется вектор, начало которого находится в начале координат выбранной системы отсчета, а конец в нашей материальной точке. Траекторией тела назовем линию, которую описывает конец радиус-вектора при движении. Пусть материальная точка в момент времени t1 находилась в точке A, в момент времени t2 переместилась в точку B. В таком случае можно ввести понятие перемещения. Перемещением s назовем вектор, начало которого лежит в точке A, а конец в точке B. Тогда, если радиус-вектор в момент времени t1 равен rA, а в момент t2 равен rB, то s = rB - rA .
Пусть вектор s имеет координаты (х, у, z) в выбранной системе отсчета. Тогда проекция его на ось Х будет равна х, на ось Y будет равна у, на ось Z будет равна z.
Другим важным понятием механики является путь. Путем называется длина траектории. Не следует путать путь и перемещение. Даже по своей сути это различные физические величины: путь — это скаляр, а перемещение — вектор. Для примера рассмотрим следующую ситуацию. Человек кидает вверх мяч, а после ловит его. При этом путь мяча не равен нулю, а перемещение равно нулю.


Вернемся к рассмотренному выше движению тела из точки A в точку B. Введем скорость движения. Скоростью v называется отношение перемещения ко времени, которое тело двигалось

Простейшим случаем механического движения является равномерное прямолинейное движение. При таком движении тело за любые равные промежутки времени совершает равные перемещения. Скорость v в этом случае постоянна.
При прямолинейном движении вместо радиус-вектора r мы можем использовать всего одну его координату, например х, если направим ось X, вдоль перемещения. Тогда проекция скорости v на ось X vx будет выражаться формулой

где х2 — конечное положение тела в момент времени t2, х1 — начальное положение тела в момент времени t1.
Другим важным случаем механического движения является равноускоренное движение. При таком движении изменение скорости v за любые равные промежутки времени постоянно. В общем случае ускорение а будет выражаться формулой

где v2 — конечная скорость в момент времени t2, v1 — начальная скорость в момент времени t1 При равноускоренном движении ускорение а есть величина постоянная. Перемещение s при равноускоренном движении будет выражаться формулой
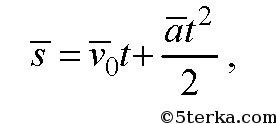
где v0 — начальная скорость тела, а —ускорение, t — время движения. Если движение происходит вдоль оси X, то зависимость координаты тела от времени будет выражаться формулой

где х0 — начальная координата тела. Также можно доказать, что проекции перемещения Sx, начальной vx1 и конечной vx2 скорости и ускорения связаны формулой

При криволинейном движении тело всегда движется с ускорением; даже если скорость по модулю постоянна, меняется ее направление. Рассмотрим теперь движение по окружности радиуса R с постоянной по модулю скоростью v. При таком движении скорость всегда направлена по касательной к траектории. Назовем периодом T время оборота на 360°, частотой v величину обратную периоду: v = 1/T. Скорость v связана с периодом и частотой формулами

Ускорение при равномерном движении по окружности называется центростремительным и обозначается ац. Как следует из названия, это ускорение направлено в центр окружности. Оно будет выражаться формулой

Приведем также формулы для вычисления ац через период T и частоту v
Приведем также формулы для вычисления ац через период T и частоту v
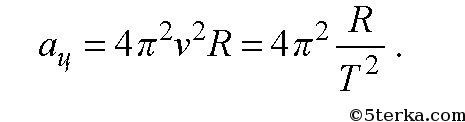
Как известно, движение нельзя рассматривать безотносительно системы отсчета. Пусть тело A в одной системе отсчета движется со скоростью v. Пусть также другое тело B в этой же системе отсчета движется со скоростью v0. Если мы перейдем в систему отсчета, связанную с телом B, то в этой системе тело A будет двигаться со скоростью v' = v — v0. Следует отметить, что любое тело в системе отсчета, связанной с самим собой покоится.