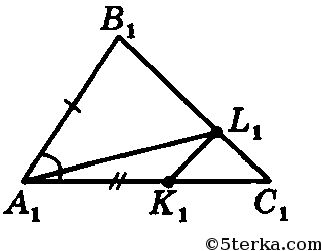
177* Даны два треугольника: ABC и А1В1С1. Известно, что АВ=А1В1, АС=А1С1, ∠A=∠A1. На сторонах АС и ВС треугольника ABC взяты соответственно точки К и L, а на сторонах А1С1 и В1С1 треугольника А1В1С1 — точки К1 и L1 так, что AK=A1K1, LC=L1C1. Докажите, что: a) KL=K1L1; б) AL=A1L1.
Из условия:


Источник:
 Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №177
к главе «Глава II. Треугольники. §4 Задачи на построение».
Комментарии